国庆节快乐!这是我的第一篇正经博客!内容是关于最近复现的一篇论文。
我的研究课题里需要做点云配准相关的工作,查了一些文献之后决定先参考这篇19年发表在 Computers & Graphics 上的论文: Fast template matching and pose estimation in 3D point clouds。 这篇论文对我的课题有比较大的参考价值。
导师建议我先复现一下看看效果,自己写一遍代码的话,对于论文的内容的了解也会加深。代码是用 VS2017 + PCL1.9.1写的,用PCL1.9.1显示点云的时候VTK会弹出警告窗口,但是如果用 VS2019 + PCL1.12.0的话似乎没有这个问题。
这篇论文的算法可以分成三个部分,第一部分是提取边缘点,第二部分是从边缘点里提取点对,第三部分是基于点对来进行RANSAC匹配。
论文中给出的流程图:
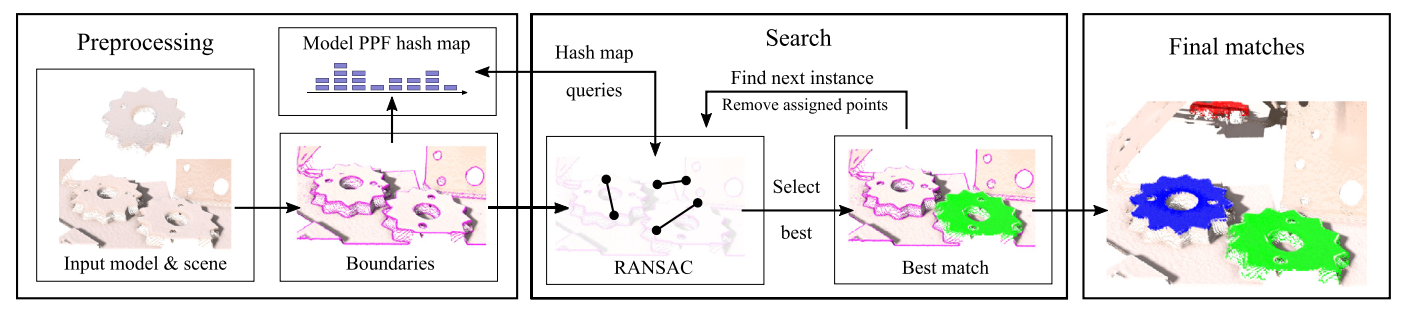
1. 边缘提取
算法的第一步就是对模板点云 (template)和待检测的场景点云 (scene)进行边缘提取。这么做可以大大减少需要处理的点云的数量,提高计算速度,同时也能保留原点云的一些独特的几何特征。边缘提取的整体流程还是比较简洁的,首先为点云里的每一个点都计算一个特征向量 (feature vector,不是eigenvector),每个向量有5个元素,也就是5个特征。第二步对这些特征向量进行k-means聚类,分为两类,一类是非边缘点,另一类就是边缘点了。
1.1 点特征计算
当我们计算某个点的几何特征的时候,一般要综合这个点和其周围点来考虑,因此在算特征之前要先给目标点圈定一个邻域,邻域半径的大小可以是点云平均密度的几倍,总之是不能太大也不能太小。
假设我们要计算特征的那个点是 $p$,邻域的半径是$r$,其邻域中点的集合是$N_r(p)$,以此来计算一个加权协方差矩阵:
\[\sum (p) = \frac{1}{|N_r(p)|}\sum_{p_i \in N_r(p)}h(||p_i-\overline{p}||)(p_i-\overline{p})(p_i-\overline{p})^T\]其中 $\overline{p}$是邻域的中点(medoid),$h()$是一个高斯窗口函数,$|N_r(p)|$指的是集合里点的总数。
协方差矩阵的三个特征值(从大到小排列)为$\lambda_1$,$\lambda_2$,$\lambda_3$,它们所对应的特征向量是$e_1$,$e_2$,$e_3$,其中前两个特征向量是在该点的切向量,而第三个特征向量为法向量。根据这三个特征值(eigenvalue),我们可以得出以下的三个点特征(feature):
- non-planarity:$f_p(p)=1-(\lambda_2-\lambda_3)/\lambda_1$
- sphericity: $f_s(p) = \lambda_3/\lambda_1$
- surface variation: $f_s(p) = \lambda_3/(\lambda_1 + \lambda_2 + \lambda_3)$
很明显,边缘点的这三个特征的值会明显高于非边缘点(脑补了一下桌子边和桌面的区别),而且它们的值都介于0和1之间。
这三个特征值的选取借鉴了Hackel等人在2016年发表的论文 Contour detection in unstructured 3D point clouds。Hackel的论文里基于特征值 (eigenvalue)计算的特征 (feature)就比较多了↓:
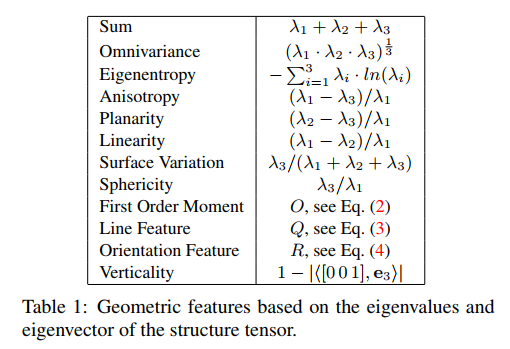
论文作者对$f_p(p)$的计算做了一个小的改动,将上图表格里的planarity改成了non-planarity,改动的目的应该是让边缘点的每个特征的值都比非边缘点的大。
剩下的两个点特征的计算借鉴了Bendels等人在2006年发表的Detecting Holes in Point Set Surfaces。其中一个是angle criterion $f_a(p)$,另一个是half-disc criterion $f_h(p)$。这两个特征在原文里被一笔带过了,不过可以参考Bendels的论文里的内容:
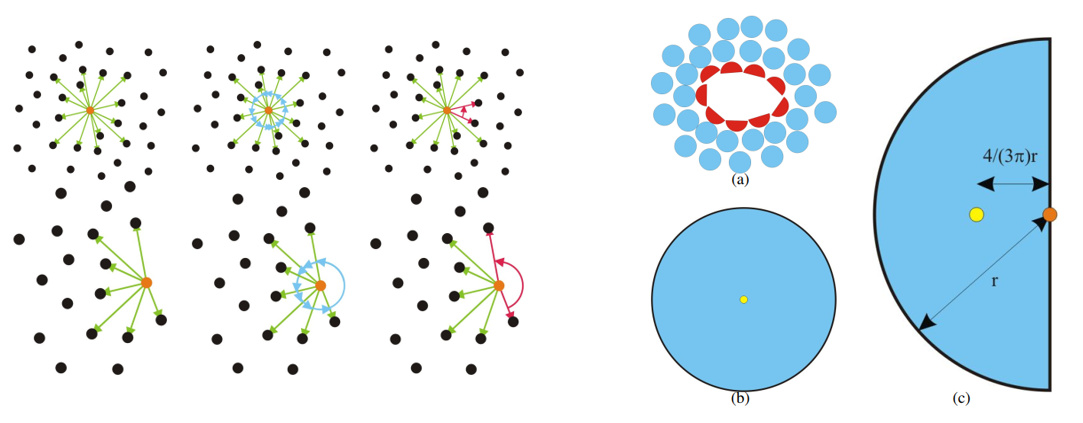
计算这两个特征之前首先需要将$N_r(p)$ 投影到一个和法向量$e_3$垂直的平面上。$f_a(p)$计算的是在投影平面上,点$p$对应的那个点到与周围点的连线之间夹角的最大值,从上图的左侧可以看出,处在边缘的点对应的最大夹角明显大于非边缘点。$f_h(p)$计算的是$p$在投影平面上和投影点的中心(centroid),也就是到周围点距离总和最短的那个点,之间的距离。从上图右侧可以看出,边缘点一般会比较偏离中心,因此这个距离会更大。
1.2 k-means 聚类
每个点的特征向量归一化之后,就可以聚类了。根据上面的分析不难看出,理论上每一个边缘点的每一个特征都应该比非边缘的点要大,因此聚类完成之后,向量的二范数更大的那一类就是边缘点。
用T-LESS dataset里面的模型测试结果:

可以看出对于个别带有圆柱面或者椭圆形状的模型,算法识别的效果不是很好,我觉得可能有两个原因,一是边缘点具有的一些特征这些点也有,二是圆柱形的物体,比如管子,它们的边缘本身就很难判定。
除了边缘点之外,后续的步骤还需要用到协方差矩阵第二大大特征值对应的特征向量$e_2$,它可以用来表示边缘的方向 (edge direction)。
Reference: