这是关于前一段时间复现的点云模板匹配论文的第二篇博客(第一篇在这里)。这篇博客的内容是如何从点云中提取用于后续匹配的点对,以及变换矩阵(transformation matrix)的计算。
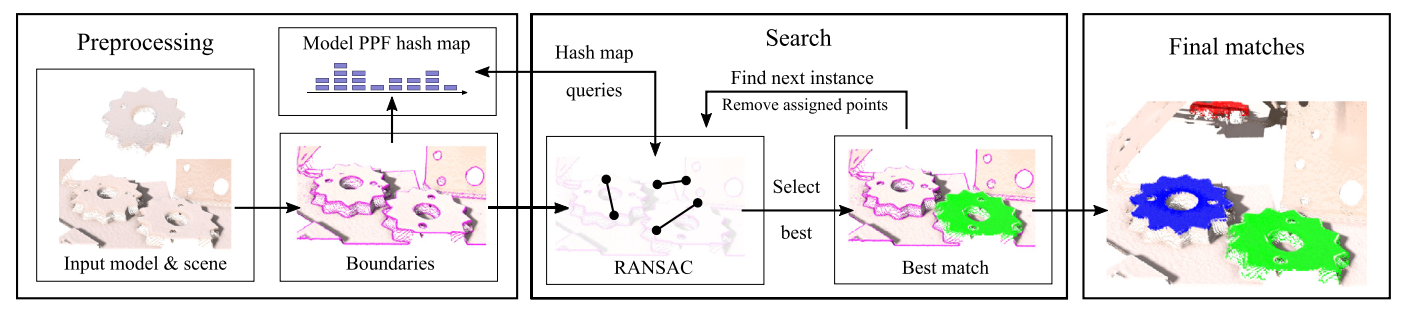
整篇论文的流程图如下:
1. 点对提取
为了降低后续RANSAC搜索耗费的时间,我们需要从点云的边缘点(edge points)中提取出能够在一定程度上代表物体几何信息的点对${p_i,p_j}$。
其中,$p_i$是在场景点云(scene cloud)的边缘点$\epsilon$中随机选取的,而$p_j$是在满足以上两个条件的情况下,在$\epsilon$中随机选取的。为了保证我们在场景点云$\epsilon$中提取的点对中至少有一个点$p_i$有$p_t$的概率($p_t$可以设为0.999之类的)落在待匹配模型的边缘点$\Psi$上,我们要提取的$p_i$的个数至少为:
\[n_1 = \frac{ln(1-p_t)}{ln(1-P(p_i \in \Psi))}\]其中$P$代表的是一个点落在待匹配模型的边缘上的概率,我们可以用待匹配模型的边缘点和场景边缘点的数量之比来表示:
\[P(p_i \in \Psi) = \frac{\vert \Psi \vert}{\vert \epsilon \vert}\]$p_j$会在$p_i$的领域内提取,我们将这个邻域的直径设为$\delta$,也就是模板点云的包围盒直径,那么$p_j$同样属于$\Psi$的概率为:
\[P(p_j \in \Psi) = \frac{\vert \Psi \vert}{\vert N_\delta(p_i)\vert}\]可以用计算$n_1$的公式来计算$n_2$。这里需要注意的是,待匹配模型的边缘$\Psi$,和模板点云的边缘$\epsilon’$之间会有差异,因为场景点云对应的是三维扫描的结果,很有可能会存在噪声,而模板点云一般是由一个完整的CAD模型得来的。不过在噪声不是很大的情况下,我们可以假设${\vert \Psi \vert} \approx {\vert \epsilon’ \vert}$。(由于光学扫描很难扫到被遮蔽的部分,如果物体之间的遮蔽区域很大的话,二者的差距就会很离谱。)
每个点对需要满足以下两个要求:
- 点与点之间的距离 $d \in [0.5\delta,0.7\delta]$。其中$\delta$是点云包围盒的直径长度。
- $p_i$的边缘方向(edge direction)与 $\overrightarrow{p_i p_j}$ 的夹角的余弦值的绝对值小于0.7:$ \vert cos(\angle(\overrightarrow{t_{p_i}},\overrightarrow{p_i p_j}))\vert <0.7 $。
2. 点对特征提取
每个点对需要提取4个特征,经过离散化之后存入哈希表里以方便后续的查询。原文的作者采用了MurMurHash3这个哈希函数。
这4个特征很容易计算,分别是:
- 点对所构成的线段长度 :$|p_i-p_j|_2$
- 点对向量与两个点处的边缘方向的夹角(在0到$\pi$之间):$\angle(\overrightarrow{p_ip_j},\overrightarrow{tp_i})$,$\angle(\overrightarrow{p_ip_j},\overrightarrow{tp_j})$
- $p_i$处的两个主曲率之比:$\kappa_2/\kappa_1$
3. 变换矩阵
点云模板匹配的最终目的就是计算出场景点到模板点的变换矩阵(为什么不是模板点到场景点呢,我想我应该会在下一篇博客里写到吧……),使模板的点能够很好地契合到场景点里。在这里我参考了Drost等人论文里的方法(他们有图,看上去更直观):
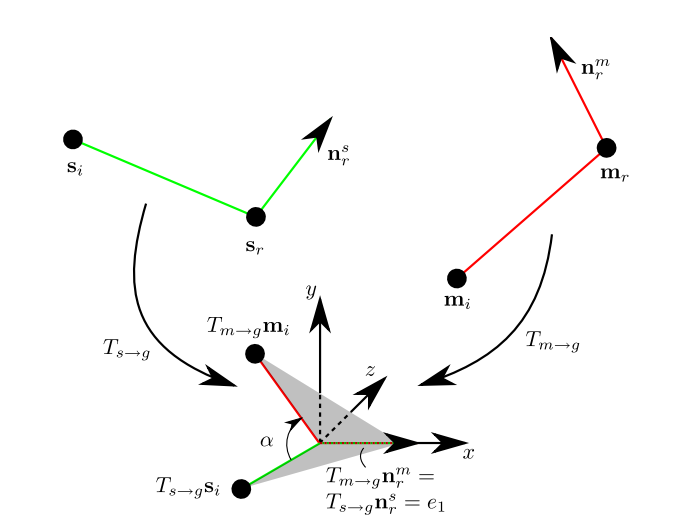
图中红色的线是一对模板点对,绿色的线是场景点对,二者端点上的箭头是法向量。首先用两个变换矩阵$T_{s\rightarrow g}$以及$T_{m\rightarrow g}$,将两个法向量转到$x$轴上,并让$s_r$和$m_r$这两个点与坐标系原点重合。接下来再计算两个点对向量之间的夹角$\alpha$,以及对应的旋转矩阵$R_x(\alpha)$。由此一来,我们就可以知道由场景点到模板点的变换矩阵为:
\[T_{s\rightarrow m} = T_{s\rightarrow g}R_x(\alpha){T^{-1}_{m\rightarrow g}}\]这样的话,就可以把比较复杂的变换矩阵计算拆分成几个相对简单的步骤。