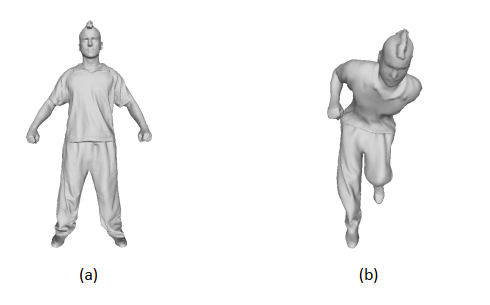
最近看了一些关于非刚性配准 (non-rigid registration)的论文。个人的理解是,非刚性配准经常会用在一些动态物体或者是会变形的物体上,配准的输入和目标虽然是同一个物体,但是它们的的形态是不一致的,比如像下面这张图,虽然这两个模型都属于同一个人,但是姿势却不一样:
找了一些顶刊的相关论文,从中先挑了最简洁(其实就是最短)的一篇读了,打算用一个很简单的笔记概括一下。
论文是2011年发表的 Locally Rigid Globally Non-rigid Surface Registration,从这篇文章的名字大致就能看出它的整体思想了,就是将一个表面看做是很多局部表面的集合,对于每个局部表面采用刚性配准,但是对于全局而言是非刚性配准。
首先作者用有向距离场(SDF)来表示源和目标形状,对于一个点$x$,和一个形状$A$,计算$\phi_A(x)$,就是$x$到$A$中离它最近的一个点的有向距离。为了节约计算时间和空间,在算SDF之前先降采样。
接下来用一个双网格FFD(free form deformation)框架来描述这个非刚性配准的问题。假设输入形状为$A$,目标形状为$B$,$A$的FFD网格会变形,而它的变形是通过网格上的控制点来控制的。除了FFD网格之外,还有一个用于采样的网格附加在FFD网格上,可以用FFD网格中的控制点来控制采样网格的形变。这两者之间的位置关系如下图(红色的是采样网格,背景灰蓝色的是FFD网格):
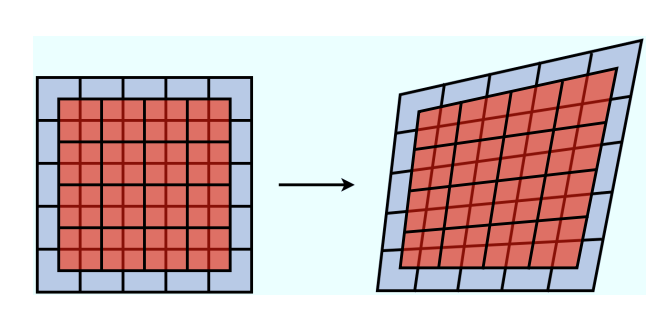
假设整体采样区域是$S$,其中的一个子区域是$s$,那么刚性变换的误差函数就可以写成这样:
\[E = \sum_{s\in S}(\phi_B(s)-\phi_A(s))^2\]通过求解$E$的最小值,就可以得出每个子采样区域的最佳刚性变换$T(s,w)$,其中$w$是刚性变化的参数。这个刚性变换$T$,是用在FFD网格里的控制点上的。因此,虽然对控制点进行了刚性变换,但是控制点的变化会使整个空间发生非刚性的变形。
此外,一个控制点的刚性变换会受到其邻域点的影响,而这个影响的大小和点之间的距离有关,距离越近,影响越大。下图解释了这个现象:
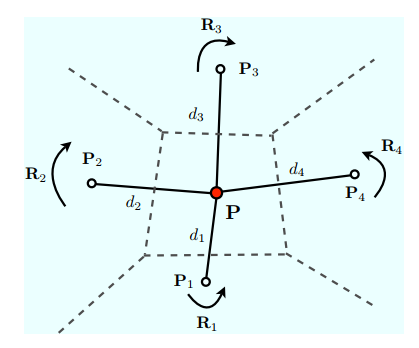
接下来就是一个迭代的过程:计算每个子区域的刚性变换$T$ -> 将这个刚性变换应用到控制点上 -> 控制点的变化引发输入形状$A$的非刚性变化 -> 计算新的刚性变换,直至收敛。
这篇论文对我而言很有参考价值,尤其是FFD的概念,我觉得很有意思,或许下一篇博客就是关于这个的吧!