一个多星期没写博客了,天气又变冷了。最近忙着写研究课题的中期报告以及选修课的报告,还感冒了……心累。还好中期报告可以用英文写,不然我可能要当场表演退学了(开玩笑的)。
这篇博客的主题是点特征直方图(PFH),是由PCL的开发者提出的。PFH是一种能够描述某个点及其k-邻域所包含的一小块区域的表面特征的描述符,它是基于点的法向量来计算的。按照原作者在PCL的指南中所写,PFH的原理是:”It attempts to capture as best as possible the sampled surface variations by taking into account all the interactions between the directions of the estimated normals.” 因此PFH的质量和法向量的估计是否准确有大的关联。
如下图所示,PFH需要计算点$p_q$的k-邻域中的所有点两两之间的关系:
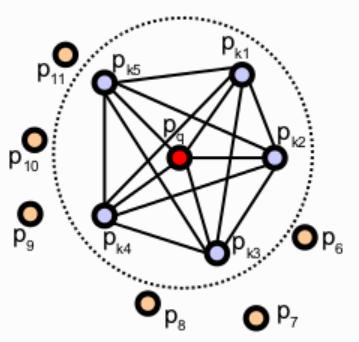
对于这个k-邻域中的每一对点${p_s,p_t}$,可以生成一个以$p_s$为原点的局部坐标系$uvw$,其中$u$轴与$p_s$点的法向量$n_s$平行,$v$轴方向为为$(p_t-p_s)\times u$轴的叉乘,而$w = u \times v$。下图就是一个例子:
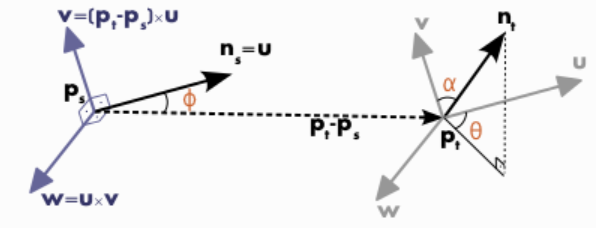
在这个基础上,我们可以针对每个点对计算一个带有四个元素的特征向量$<\alpha,\phi,\theta,d>$。其中$d$是$p_s$和$p_t$之间的距离,$\theta = \arctan(w \cdotp n_t, u \cdotp n_t)$,其他的两个特征的计算方法可以直接从上图看出来。
在此之后,每个点对应的四个特征都被分散到$b$个子区间里,通过统计k-邻域中所有点的特征在这$b$个区间里出现的次数,就可以画出该点对应的直方图。在编程的时候#include <pcl/features/pfh.h>并调用pcl::PFHEstimation这个类,就可以计算PFH了。
由于计算一个点的PFH时,需要计算k-邻域中每个点和其余所有点组成的点对的特征向量,因此它的复杂度为$O(n^2)$。为了降低复杂度作者提出了一个简化版本,即为 fast point feature histogram (FPFH)。
每个点对只计算$<\alpha,\phi,\theta>$这三个特征,这个简化后的特征被称为simplified PFH (SPFH)。在计算一个点$p_q$的SPFH时,只考虑$p_q$和其邻域中的点组成的点对,由此复杂度从$O(n^2)$降到了$O(n)$。最终的FPFH由以下公式计算得到:
\[FPFH(p_q) = SPFH(p_q) + \frac{1}{k}\sum_{i=1}^k \frac{1}{\omega_i} \cdotp SPFH(p_i)\]其中$\omega_i$代表$p_i$的权重,对应了$p_q$和$p_i$之间的距离。
FPFH的示例图如下图所示,其中红色的点标出了计算$p_q$的SPFH所需要的点对,对应了上式等号右边的第一项。而用黑线表示的是需要进行额外加权操作的点对,对应了上式等号右边的第二项,其中有些点对在第一项和第二项里各被用了一次,用加粗的黑线表示。
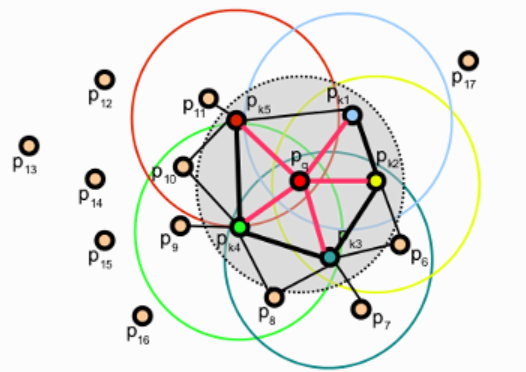
与PFH相比,FPFH不仅在计算复杂度上有所降低,同时也简化了结果的表示,因为每个点只有一个FPFH。某个点的FPFH可能会考虑与其距离大于邻域的半径的点,不过这个距离不会大于2倍的半径。
第一次接触PFH大概是在一年前,那个时候我正在休学实习,在点云处理方面还是个完全的新手,看得云里雾里的。过了一年再回头看这个概念,发觉其实并不难。这说明这一年里多少还是有点进步的吧。