[
code
]
字典树(Trie tree)又称为前缀树,可以高效地存储和查询大量字符串。字典树结构的一个例子如下图(来自维基百科)。
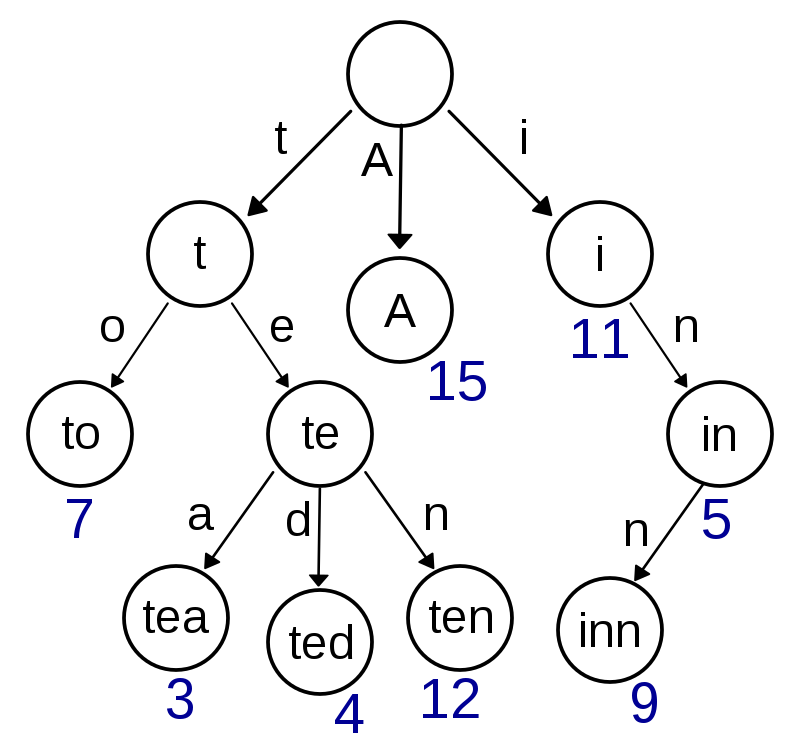
我最近在做leetcode第208题的时候接触到了字典树的概念。以这道题为例:在字典树中,除根节点之外,每个节点都代表一个字符,并且包含一个布尔量”isEnd”来表明该节点是否是某一个字符串的终点,如果是的话,布尔量的值为true。此外,每个节点还包含了一个数组用于存储其指向的子节点。这样一来,从根节点开始到任意一个终点节点的路径就组成了一个字符串。从图中可以看出,具有公共前缀的字符串,比如最右侧的”in”和”inn”,共享了路径。这样能够提高存储和查询的效率。需要注意的是,在字典树中,终点节点不一定是叶子节点。比如”in”的”n”所在的节点不是叶子节点。
插入
向字典树中存入一个字符串a时,首先查询与根节点连接的节点中是否有节点包含a的第一个字符a[0]。如果没有,那就创建一个包含a[0]的新节点与根节点连接,并在该节点之后依次创建包含a[1], a[2],…, a[n-1]的新节点;如果有,那就顺着该节点继续重复以上步骤。最后,需要将代表a[n-1]的终点节点中的”isEnd”设为true。
查询
查询字典树中是含有字符串a时,从根节点开始,沿着路径依次查询是否包含a中的各个字符,如果有一条从根节点开始的路径能够代表a,且该路径的最后一个节点的”isEnd”值为true,那么字典树中包含a。
打了这么多字还是觉得有点乱乱的,下面就直接放leetcode 208题的代码吧:
class Trie {
public:
Trie() {
isEnd = false;
//字典树中只包含小写字母,因此next矩阵的大小为26
for(int i = 0;i<26;i++)
{
//initialize
next[i] = nullptr;
}
}
//插入
void insert(string word) {
Trie* root = this;
int tmp;
for(char it: word)
{
tmp = it-'a';
if(root->next[tmp] == nullptr)
{
//如果子节里不包含相应的字符,就新建一个子节点
Trie* node = new Trie();
root->next[tmp] = node;
}
root = root->next[tmp];
}
root->isEnd = true;
}
//查找单词
bool search(string word) {
Trie* root = this;
int tmp;
for(char it: word)
{
tmp = it-'a';
if(root->next[tmp] == nullptr)
return false;
root = root->next[tmp];
}
return root->isEnd;
}
//查找公共前缀
bool startsWith(string prefix) {
Trie* root = this;
int tmp;
for(char it: prefix)
{
tmp = it-'a';
if(root->next[tmp] == nullptr)
return false;
root = root->next[tmp];
}
return true;
}
private:
bool isEnd; //节点是否是某个单词的结尾
Trie* next[26]; //该节点指向的子节点
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/