本篇博客记录了原始-对偶(Primal-Dual)方法,是上一篇博客线性规划的对偶问题的扩展。内容主要来自这学期选修的一门课程以及网络上的资料。
同上一篇博客一样,以下称原线性规划问题为LP1,其对偶线性规划为LP2,二者的基本形式如下:
LP1:
Input: $A$, $b$, $c$
Output: $x \in \mathbb{R}$
Constraint: $A \cdot x \geq b$
Objective funtion: $\min(c \cdot x)$
LP2:
Input: $A$, $b$, $c$
Output: $y \in \mathbb{R}$
Constraint: $A^T \cdot y \leq c^T$
Objective funtion: $\max(b^T\cdot y)$
原始-对偶线性规划(Primal-Dual LP)
在写primal-dual方法之前,先回顾一下对偶线性规划的互补松弛性(complementary slackness):
假设LP1的解为$x$,LP2的解为$y$,如果此时$y$中的某个变量$y_i$的值大于0,那么其在LP1中对应的约束条件中的符号应为等号,即: $\sum_{j=1}^{n} a_{ij}x_j = b_i$,此时我们称这个约束是紧的。假如$y_i=0$,那么LP1中对应的约束应该取不等号,即:$\sum_{j=1}^{n} a_{ij}x_j > b_i$,此时这个约束是松的。
Primal-Dual方法从对偶LP的可行解出发, 在满足互补松弛条件的前提下, 使得原始变量朝着可行解的方向迭代。在此用课堂上一道比较简单的例题来帮助理解。
例题:支配集(dominating set)问题
假设有一个如下图所示的社交网络$S=\left\{V,E\right\}$,其中$V$代表人,$E$中存放社交关系(举个例子,图中1和2是朋友,那么$\left\{1,2\right\} \in E$)。我们需要在这群人中选出一个子集$S$,在使$S$中人数尽可能少的同时,让我们可以通过$S$联系到$V$中所有的人。由此可知,在一个可行解中,$V$中的每个人$v_i$要么属于$S$,要么是$S$中某个人的朋友。
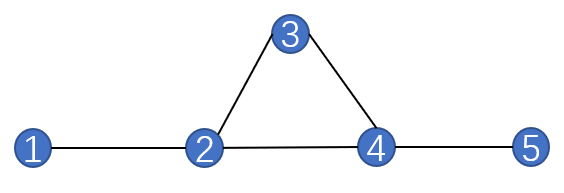
于是写出线性规划问题LP1:
Input:$V$, $E$
Output: $x_1,…,x_5 \in \left\{0,1\right\}$,代表是否选择第$i$个人到子集$S$里。
Constraint: $Ax \geq b$
Optimization function: $\min(cx)$
其中
\[A =\left[ \begin{array}{ccccc} 1&1&0&0&0\\ 1 &1& 1& 1& 0\\ 0 &1 &1& 1& 0\\ 0 &1& 1& 1& 1\\ 0 &0 &0& 1& 1\end{array} \right], b = \left[ \begin{array}{c} 1\\ 1 \\ 1\\ 1 \\ 1 \end{array} \right], c = b^t\]它的对偶线性规划LP2为: Output: $y_1,…,y_5$
Constraint: $A^ty \leq c^t$
Optimization function: $\max (b^ty)$
我们用Primal-Dual方法来求解这个线性规划问题。根据互补松弛性,若$x_i > 0$,那么$A^{(i)}y = c_i$,为紧约束;当$y_i > 0$时,$A_ix = b_i$。
Primal-Dual方法的流程如下:
- 给$x$和$y$中每个元素赋初始值0。
- 从$y$中选取一个不存在于任何紧约束中的变量$y_{i’}$。
- 增大$y_{i’}$,直到它让一些LP2中的约束由松变紧。用$j_1,…,j_k$来表示这些约束。
- $x_{j_i} \leftarrow 1,…,x_{j_k} \leftarrow 1$。
- 如果此时$x$满足了LP1的约束条件,终止迭代,反之跳到第2步。
该方法是一个N-近似方法,N为最多可拥有的朋友数量+1。
例题2:健壮的网络设计(Survivable network design)
我其实不清楚如何把survivable翻译成中文,个人认为这个词是对干扰的鲁棒性较高的意思。
假设我们有如下的一个网络,其中每个圆代表一个传感器,方块代表基站,基站和传感器,传感器和传感器之间可以互相传递信息,而建立每条信息同道需要花费一定的代价(标在了直线上,代价等于直线的编号)。我们想要在尽量减少代价的同时,令基站向所有传感器发送信息,且当随机一条线路损毁的时候,信息的传递不受影响。
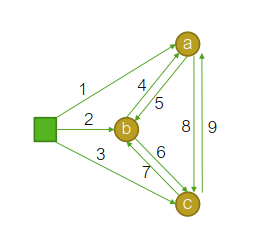
写出如下的线性规划问题LP1:
Input: 基站,传感器集合$V$,所有可建立的连接$l=[l_1,l_2,…,l_9]$,及对应的代价$c = [1,2,…,9]$。
Output: 需要建立的连接 $x = [x_1,x_2,…,x_9]^t, x\in \{0,1\}$。
Constraint: 基站必须能够向所有传感器发射信息,即便有一条路线毁坏。即在传入任意一个传感器集合的路径中,必须至少有两条路是通的。以传感器$a$为例,其对应的限制条件是:$x_1+x_4+x_9 \geq 2$;如果将$a,b$看做是一个传感器集合,其对应的限制条件是:$x_1+x_2+x_7+x_9 \geq 2$。
Optimization function: $\min(cx)=\min(x_1+2x_2+…+9x_9)$
写完之后发现有个问题,那就是限制条件的数量是$2^n$,其中$n$是传感器的数量。如果我们有很多传感器,那么限制条件也会变得特别多(这一点和例题1很像)。
接下来我们对算法进行一下简化,将“当随机一条线路损毁的时候,信息的传递不受影响”这个条件去掉,换句话说,就是把约束条件不等号右边的2变为1,这个简化后的问题用LP1’表示。此时,我们可以用Edmond算法(可以参考这里)快速地解决它。Edmond算法解出的路径编号集合为 $S=\{1,2,3\}$,即为基站到传感器的三条路径。
随后,我们查找$S$是否满足LP1中的一些约束条件,并移除这些条件。
LP1中的约束条件如下:
\[x_1+x_4+x_9 \geq 2 \\ x_2+x_5+x_7 \geq 2 \\ x_3+x_6+x8 \geq 2\\ x_1+x_2+x_7+x_9 \geq 2\\ x_1+x_3+x_4+x_6 \geq 2\\ x_2+x_3+x_5+x_8 \geq 2\\ x_1+x_2+x_3 \geq 2\]$S$能够满足除了前三个之外的不等式。我们去除已被满足的约束,剩下未被满足的约束:
\[x_4+x_9 \geq 1\\ x_5+x_7 \geq 1\\ x_6+x_8 \geq 1\]这三个不等式分别对应$a,b,c$三个单独的节点。针对余留下的约束,我们写出如下的线性规划LP2及其对偶线性规划LP3:
LP2
Input, output, constraint参照前文。
Optimization function: $\min(4x_4+…+9x_9)$
LP3
Input: 参照前文
Output: $y = [y_a,y_b,y_c]$
Constraint:
\[y_a \leq 4\\ y_a \leq 9\\ y_b \leq 5\\ y_b \leq 7\\ y_c \leq 6\\ y_c \leq 8\]Optimization function: $\max(y_a+y_b+y_c)$
然后,采用Primal-Dual方法来解决问题。首先将剩余的每个最小传感器集合(其实就是单个传感器)中变量的值变为4,此时LP3的第1个约束变紧,对应LP2中$x_4$值变为1。接下来将$y_a$去掉,剩下的值变为5,此时LP3中第3个约束变紧,对应LP2中$x_5$的值变为1。最后去掉$y_b$,令剩下的$y_c$值变为6,对应$x_6$变为1。
由此可知,最后求得的LP1的解为$S=\{1,2,3,4,5,6\}$。
例题2中算法的整体步骤如下:
- 用Edmond算法解决简化后的问题,算法的结果为$S$。对$S$中的每一个元素$i$,令$x_i = 1$。
- 移除原问题中已被满足的约束条件。
- 用Primal-Dual方法使解满足剩下的条件。
3.1.令剩余的约束条件为$C = \{c_1,…,c_p\}$。若$C = \emptyset$,终止算法。剩余的对偶变量为$y_{c_1},…,y_{c_p}$。$C$的最小子集的集合为$C’$。
3.2. 对于$C’$中的每个最小子集$c$,增大$y_c$的值,直到第$i$个约束变紧。
3.3. $x_i \leftarrow 1$,移除被满足的约束,跳回步骤3.1.
其实我对于“最小子集”这个概念有些不太明白,老师在课堂资料上写的原文是”minimal set”,结合题目之后我的理解是,这个所谓的minimal set应该就是指单个的传感器吧。