周一连着考了两场试,这学期的课程算是结束了,可以稍微放松一下了。
本篇博客的内容是查找和排序算法。这应该是相对基础的算法知识了,然而我总是记不住,每次看见排序的题目就头大,于是打算趁着春节前的这几天再重新总结一遍。
排序算法
以下算法排序时默认采用升序:
1. 冒泡排序
冒泡排序是一种比较简单的排序算法(学C++基础的时候都会讲到这个吧),它的过程是:
-
从头到尾遍历数组里的每个元素,如果发现两个相邻元素的大小关系不符合要求,就交换这两个元素的位置。当一次遍历完成之后,在数组末尾的元素应该是被遍历元素中最大/最小的元素(取决于是升序还是降序排列),它的位置就固定住了。
-
重复步骤1,在上一次遍历的最后一个元素前停止,直到所有元素都排序完成。
假设数组里有$n$个元素,冒泡排序每次都确定至少一个元素的位置,那么需要遍历数组$n-1$次,其中第$i$次遍历的元素数量为$n-i$($i$从0开始计数),算法时间复杂度是$O(n^2)$,空间复杂度是$O(1)$。冒泡排序是稳定的。所谓稳定性就是指,假设在原数组中有两个元素$a = b$,且排序后$a$和$b$的相对次序没有变,则该算法是稳定的,否则是不稳定的。
代码如下:
//升序
void bubble_sort(vector<int>& arr)
{
int n = arr.size();
for (int i = 0; i < n - 1; i++) //遍历的次数
{
for (int j = 0; j < n - 1 - i; j++) //每次遍历的元素
{
if (arr[j] > arr[j + 1])
{
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
return;
}
2. 插入排序
同时也是一种比较简单的排序算法。插入排序(升序)的过程如下:
-
取出数组中的第$i$个元素(从0开始计数,$i$的初始值为1),并将它与之前的元素进行比较。如果找到了一个小于它的元素$a$(降序排列的话就是大于),就将第$i$个元素插入到$a$的后面,如果没有找到,就将第$i$个元素放在最前面。
-
$i=i+1$,重复步骤1,直到遍历完数组最后一个元素。
如果通过在原地修改数组来实现排序的话,每次插入的时候需要将部分元素向后移1位。插入排序的时间复杂度为$O(n^2)$,空间复杂度是$O(1)$,是稳定的排序算法。
代码如下:
//升序
void insertion_sort(vector<int>& arr)
{
int n = arr.size();
for (int i = 1; i < n; i++) //每次插入的元素
{
int tmp = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > tmp)
{
arr[j + 1] = arr[j]; //后移一位
j--;
}
arr[j + 1] = tmp;
}
return;
}
当数组元素数量比较多的时候,以上两个$O(n^2)$的算法就显得有些麻烦了。
3. 归并排序
归并排序采用了分治(divide and conquer)的思想,它递归地地将数组一分为二,对分裂出的子数组进行排序,最后将排序好的子数组合并在一起,我画了一张简单的图来解释这个过程:
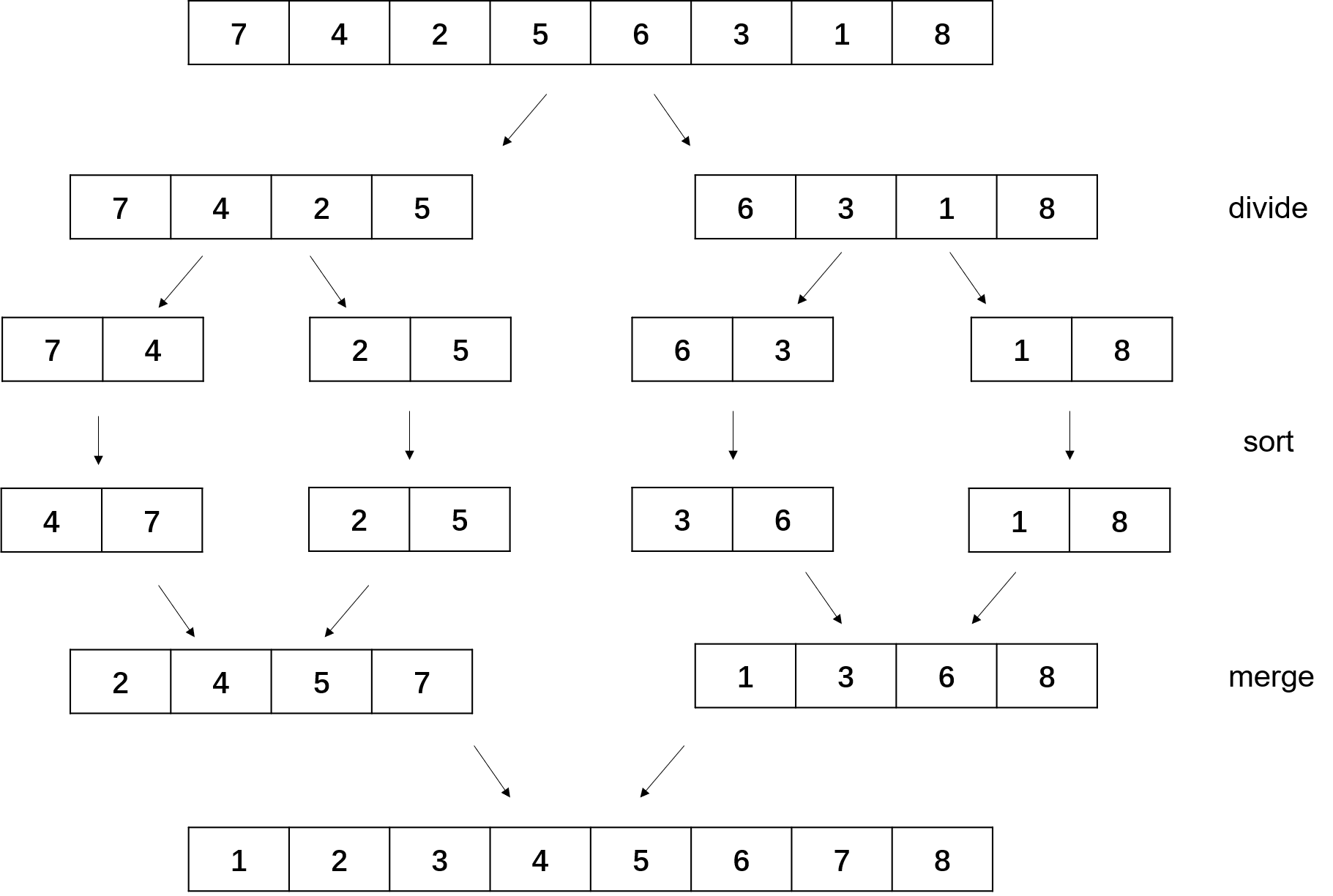
在合并子数组的时候,首先让两个指针分别指向子数组的第一个元素,将较小的元素存入合并后的数组中,并将其对应的指针后移一位。最后不断的重复这个操作直到某个指针率先事先到达数组末位,再将另一个数组中没有被遍历到的元素挨个存进去即可。
归并排序的时间复杂度是$O(n\log_2 n)$,空间复杂度是$O(n)$,是一种稳定的算法。它需要开辟额外的空间来存放分裂后的子数组。
代码如下:
void merge_sort(vector<int>& arr, int st, int ed)
{
int n = ed - st + 1;
if (n > 2) //子数组有多于2个元素
{
merge_sort(arr, st, st + n / 2);
merge_sort(arr, st + n / 2 + 1, ed);
merge(arr, st, ed);//合并两个数组
}
else if (n == 2 && arr[st] > arr[ed])
{
int tmp = arr[st];
arr[st] = arr[ed];
arr[ed] = tmp;
}
return;
}
//将st-ed部分的两个子数组合并
void merge(vector<int>& arr, int st, int ed)
{
int i1 = st;
int m = st + (ed - st + 1) / 2;
int i2 = m + 1;
int i3 = 0;
vector<int> rtn(ed - st + 1);
while (i1 <= m && i2 <= ed)
{
if (arr[i1] <= arr[i2])
{
rtn[i3++] = arr[i1++];
}
else
{
rtn[i3++] = arr[i2++];
}
}
while (i1 <= m)
{
rtn[i3++] = arr[i1++];
}
while (i2 <= ed)
{
rtn[i3++] = arr[i2++];
}
//合并后的结果复制回arr
copy(rtn.begin(), rtn.begin() + ed - st + 1, arr.begin() + st);
return;
}
一个更复杂的例子:数组中的逆序对
这道题来自于剑指offer,可以借助归并排序解决,但是很难将它与归并排序联系起来(反正我想不出来):在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
那么怎么解这道题呢?假设输入是上面图中的数组,我们首先对其进行归并排序,在合并的过程中,有两个待合并的数组$l = [2,4,5,7]$以及$r=[1,3,6,8]$。这两个数组已经被排序好了,且一个代表了原数组的前半部分,另一个代表了后半部分。可以看出,$l[1]$比$r[0],r[1]$大,比$r[2]$及其之后的元素要小,因此$l[1]$和$r$中的元素能够组成2个逆序对。由此类推,$l[2]$和$r$中元素能够组成2个逆序对,$l[3]$可以组成3个。
在归并排序的代码中,我们采用了以下的方法来比较并拼接两个已排序的数组中的元素:
int i1 = st;
int m = st + (ed - st + 1) / 2;
int i2 = m+1;
int i3 = st;
while (i1 <= m && i2 <= ed)
{
if (arr[i1] <= arr[i2])
{
rtn[i3++] = arr[i1++];
}
else
{
rtn[i3++] = arr[i2++];
}
}
其中,左数组元素的范围是$st$到$m$,而右子数组范围是$m+1$到$ed$,$i_1$和$i_2$分别指向目前左数组和右数组元素的位置。若代码中的第一个if循环的条件为true,即$arr[i_1] \leq arr[i_2]$,那么在右数组中,所有排在$arr[i_2]$之前的元素均比$arr[i_1]$小,此时$arr[i_1]$有$i_2-m-1$个逆序对。由此,我们对归并排序的代码稍作修改就可以计算出数组中逆序对的数量。
代码:
class Solution {
public:
int merge_sort(vector<int>& arr, int st, int ed)
{
int num = 0;
int n = ed - st + 1;
if (n > 2) //子数组有多于2个元素
{
num = merge_sort(arr, st, st + n / 2)+merge_sort(arr, st+n/2+1, ed);
num += merge(arr, st, ed);//合并两个数组
}
else if(n == 2 && arr[st] > arr[ed])
{
int tmp = arr[st];
arr[st] = arr[ed];
arr[ed] = tmp;
return 1; //有一个逆序对
}
return num;
}
//将st-ed部分的两个子数组合并
int merge(vector<int>& arr, int st, int ed)
{
int num = 0;
int i1 = st;
int m = st + (ed - st + 1) / 2;
int i2 = m+1;
int i3 = 0;
vector<int> rtn(ed-st+1);
while (i1 <= m && i2 <= ed)
{
if (arr[i1] <= arr[i2])
{
rtn[i3++] = arr[i1++];
num += (i2-(m+1));
}
else
{
rtn[i3++] = arr[i2++];
}
}
while (i1 <= m)
{
rtn[i3++] = arr[i1++];
//此时右数组中每个元素都与其构成逆序对
num += (ed-m);
}
while (i2 <= ed)
{
rtn[i3++] = arr[i2++];
}
//合并后的结果复制回arr
copy(rtn.begin(),rtn.begin()+ed-st+1,arr.begin()+st);
return num;
}
int reversePairs(vector<int>& nums) {
int n = nums.size();
return merge_sort(nums,0,n-1);
}
};
4. 快速排序
快速排序也采用了分治的思想。首先选取一个值作为基准值,并将大于基准值的元素放在基准值之前,将小于基准值的元素放在基准值之后。随后,对前后部分递归地重复先前的步骤。
快速排序的平均时间复杂度为$O(n\log_2 n)$,空间复杂度为$O(n \log_2 n)$,是不稳定的。
代码如下:
int partition(vector<int>& arr, int st, int ed){
int i = st, j = ed, x = arr[st]; //将最左元素记录到x中
while (i < j)
{
// 从右向左找第一个<x的数
while(i < j && arr[j] >= x)
j--;
if(i < j)
arr[i++] = arr[j]; //移到左边
// 从左向右找第一个>x的数
while(i < j && arr[i] <= x)
i++;
if(i < j)
//移到最右边
arr[j--] = arr[i];
}
arr[i] = x; //i的左侧元素小于x,右侧元素大于x
return i;
}
void quick_sort(vector<int>& arr, int st, int ed)
{
if (st>=ed)
{
return; //排序完成
}
// 分割数组,找出基准点
int i = partition(arr, st, ed);
quick_sort(arr, st, i - 1);
quick_sort(arr, i + 1, ed);
return;
}
5. 希尔排序(Shell Sort)
希尔排序是插入排序的加强版,其平均时间复杂度为$O(nlog_2n)$,空间复杂度是$O(1)$,是不稳定的排序算法。
在插入排序中,每次只能将数字移动一位,而在希尔排序中,假设数组长度为$n$,那么在一开始,我们将数组分为$n/2$组,第$i$个元素和第$i+n/2$个元素为一组,我们比较二者的大小,后者较小则交换位置。接下来我们不断地将分组长度除以2(相应的每组元素数量乘2),并分组进行插入排序。当步长变为1时,希尔排序就等同于插入排序。
以下是代码:
void shell_sort(vector<int>& nums)
{
int n = nums.size();
for (int k = n / 2; k > 0; k /= 2) //步长的长度
{
for (int i = 0; i < k; i++) //比较位于i和i+k的数
{
for (int j = i + k; j < n; j += k)
{
int tmp = nums[j];
int pre = j - k;//要对比的元素
//进行插入排序
while (pre >= 0 && nums[pre] > tmp)
{
//交换位置
swap(nums[pre], nums[j]);
pre -= k;
}
nums[pre + k] = tmp;
}
}
}
return;
}
查找算法
1. 二分查找
二分查找的对象应该是一个已经排序好的数组。二分查找经常会被用于查找某个数,或者查找左右边界。过程比较简单(就是不停地用二分法),但是有很多细节需要注意,比如中值的选择,终止条件等等。以下是两个使用二分查找的例子:
例1:查找特定值
给定一个长为$n$,没有重复元素的数组$num$,我们需要在数组中找到某个特定值$target$的索引,如果数组中不存在这个值,那么返回-1。
解决这个问题的方法就是首先将数组排序,左右边界分别初始化为$0$和$n-1$,随后采用二分法不断地取左右边界中间的那个值$num[mid]$与目标值比较,如果$num[mid]<target$,说明目标值在$mid$右边,令左边界等于$mid+1$,如果$num[mid]>target$,说明目标值在$mid$左边,令右边界等于$mid-1$,如果$num[mid]=target$,那么直接返回。如果一直迭代到左右边界叠一块了都没有找到目标值,说明数组中不包含该值。
代码:
int binary_search(vector<int> num, int target)
{
int left = 0;
int right = num.size() - 1;
while (left < right)
{
int mid = left + (right - left) / 2;
if (num[mid] == target)
return mid;
else if (num[mid] < target)
left = mid + 1;
else
right = mid - 1;
}
return num[left] == target ? left : -1;
}
例2:查找特定值所处的范围
给定一个长为$n$,含有重复元素的,已经排列好的数组$num$,我们需要在数组中找到某个特定值$target$所处的范围,如果数组中不存在这个值,那么返回$[-1,-1]$。这比查找单个元素的情况要稍微复杂一点,我们需要分别找出元素所处范围的左右边界。注意在查找过程中,区间是左闭右开的,所以右边界的初始值为$n$而非$n-1$。 代码:
vector<int> binary_search2(vector<int> num, int target)
{
int left = 0;
int right = num.size();
vector<int> rtn = { -1,-1 };
//先找左边界
while (left < right)
{
int mid = left + (right - left) / 2;
if (num[mid] < target) //说明mid在左边界的左边
left = mid + 1;
else //说明mid在右边界上或右边界的右边
right = mid;
}
if (num[left] != target)
return rtn; //不包含target
rtn[0] = left;
//找右边界
right = num.size();
while (left < right)
{
int mid = left + (right - left) / 2;
if (num[mid] <= target)
left = mid + 1;
else //说明mid在右边界的右边
right = mid;
}
rtn[1] = right - 1; //此时我们找到的应该是右边界的下一位,所以需要-1
return rtn;
}
2. 插值查找
插值查找的流程和二分查找差不多,区别在于,插值查找每次选取位置的时候,并不是像二分查找那样严格地选取左右边界的中间位置,而是根据左右边界的值与目标值$target$来自适应地选取。
插值查找同样要求待查找的数据是已经排列过的,插值查找的时间复杂度是$O(\log_2(\log_2 n))$。
代码如下:
int insertion_search(vector<int> num, int target)
{
int left = 0, right = num.size() - 1;
while (left < right)
{
//根据当前边界值选取下一次的边界
int mid = left + (right - left)*(target - num[left]) / (num[right] - num[left]);
if (num[mid] == target)
return mid;
if (num[mid] < target)
left = mid + 1;
else
right = mid - 1;
}
return num[left] == target ? left : -1;
}
3. 二叉搜索树(Binary Search Tree)
我们可以用待查找的数据生成一棵二叉搜索树。二叉搜索树是一种特殊的二叉树,其中任意一个节点满足以下两个条件:
-
对于任意一个非叶子节点,如果左子树非空,则左子树上的所有节点的值均小于该节点的值;如果右子树非空,则右子树上所有节点值均大于该节点的值。
-
每个非叶子结点的左右子树也是二叉搜索树。
二叉搜索树的查找与插入的时间复杂度与其是否平衡有关(就是左右子树的节点数量是否平衡),其时间复杂度为$O(\log_2 n)$~$O(n)$。
在二叉搜索树中查找元素时,若当前结点的值小于目标值,那么继续搜索其右子树,若当前结点的值大于目标值,则搜索其左子树。插入和删除就相对要麻烦一些了,尤其是当目标位置不在叶子节点上的时候。
在这里用剑指offer中的一道题展示一个二叉搜索树的简单应用。
例1. 二叉搜索树中第k大的节点
根据二叉搜索树的性质可知,如果我们对其进行中序遍历(即左子节点→根节点→右子节点),得到的序列是升序的,进行后序遍历(即右子节点→根节点→左子节点)得到的序列是降序的。如果想要获得第k大的节点,那么可以进行后序遍历。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int kthLargest(TreeNode* root, int k) {
//后序
nums = 0;
search(root,k);
return num;
}
void search(TreeNode* node, int k)
{
if(node == nullptr)
return;
else
{
//后序
search(node->right,k);
if(++nums == k) //遍历到了第k个数
num = node->val;
search(node->left,k);
}
return;
}
int num,nums;
};
待续……
Reference
- 十大经典排序算法
- 数组中的逆序对
- 快速排序
- 七大查找算法
- 二叉搜索树的第k大节点
- 剑指offer