居然已经快一个月没有写新博客了，这段时间在steam和switch二者的陪伴下我渐渐地变得乐不思蜀了起来……咳咳，最近的研究课题没有什么明显的进展，也没有学到特别多的新知识，但是博客还是坚持更新比较好。

本篇博客的内容是树形动态规划，顾名思义，就是在基于树的数据结构做动态规划，一般是在一棵树上选出某些结点，作为问题的最优解。动态规划相关的一些定义如下（来自百度百科）：

动态规划：

问题可以分解成若干相互联系的阶段，在每一个阶段都要做出决策，全部过程的决策是一个决策序列。要使整个活动的总体效果达到最优的问题，称为多阶段决策问题。动态规划就是解决多阶段决策最优化问题的一种思想方法。

阶段：

将所给问题的过程，按时间或空间特征分解成若干相互联系的阶段，以便按次序去求每阶段的解。

状态：

各阶段开始时的客观条件叫做状态。

决策：

当各段的状态取定以后，就可以做出不同的决定，从而确定下一阶段的状态，这种决定称为决策。

策略：

由开始到终点的全过程中，由每段决策组成的决策序列称为全过程策略，简称策略。

状态转移方程：

前一阶段的终点就是后一阶段的起点，前一阶段的决策选择导出了后一阶段的状态，这种关系描述了由k阶段到k+1阶段状态的演变规律，称为状态转移方程。（我认为这是动态规划问题里最难的部分，一般只要求得状态转移方程，问题就解决了大半，但是有时候状态转移方程的规律很难找。）

一个简单的线性动态规划实例

这里以一个简单的爬楼梯问题为例：假设我们要总共要爬$n$层楼梯，每次可以爬1或2层，爬到每一层需要不同的体力值，存储在数组$cost$里。我们需要求出爬到第$n$层所消耗的最小体力值。

为了解决这个问题，我们可以用一个长度为n的数组$dp$来记录爬到每一层所消耗的最小体力，其中$dp[i]$表示爬到第$i$层所消耗的最小体力。很容易可以知道$dp[0]=cost[0]$，$dp[1] = cost[1]$。而针对更高的楼层，我们只能从第$i-1$层或第$i-2$层爬上去，由此写出如下的状态转移方程：

想要求得爬到第n层所需的最小体力，只需要根据以上的状态转移方程，遍历 $0$ ~ $n-1$层，依次求出对应的dp值，最后返回$dp[n-1]$即可。

树形动态规划

由于树形动态规划是基于树形结构的，它的遍历方式比上述线性动态规划的例子要复杂。树形dp的遍历有两种方向，一种是从根节点到叶子节点，另一种是从叶子节点到根节点（用得多一些），往往需要用到递归以及记忆化搜索。

以下是一道leetcode上的树形动态规划例题 二叉树染色：

有一个根节点为$root$的二叉树模型，初始所有结点为白色，每个结点有一个对应的价值$val$，可以用蓝色颜料给结点染色。为了美观，希望最后二叉树上每个蓝色相连部分的结点个数不能超过$k$个(取值范围为1~10)，求所有染成蓝色的结点价值总和的最大值。

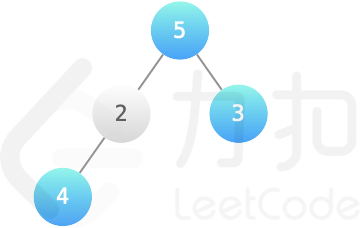
一个简单的例子如下，此时$k=2$，因此最多只能有2个蓝色结点相连。则最大价值总和为5+3+4=12。

我们可以用一个长度为$k+1$的数组$dp$来记录状态，其中$dp[i]$代表以当前节点为根节点，且最大相连结点个数为$i$时，所获得的最大价值总和。状态转移的过程分析如下：

当$i=0$时，表示当前节点是白色，此时$dp[i]$的值等于该节点的左右子树中，蓝色结点最大价值的总和，即：

当$i \geq 1$时，当前节点是蓝色，且有$i-1$个蓝色结点与其相连，蓝色节点的分布有$i$种情况：左边连着$j (0 \le j \le i-1)$个蓝色结点，右边连着$(i-j-1)$个。此时的状态转移方程为：

初始状态下，$dp[i]=0$，我们选择从叶子节点->根节点的遍历方向来更新每一层结点对应的dp值，最终返回根节点对应的所有染色状态的最大值$max(dp)$。

我们用深度优先搜索（DFS）来解决这个问题，代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxValue(TreeNode* root, int k) {
       vector<int> dp = dfs(root, k);
        return *max_element(dp.begin(), dp.end()); //返回dp中的最大值
    }
	
    vector<int> dfs(TreeNode* root, int k) {
        vector<int> dp(k + 1, 0); //初始化
        if (!root) 
			return dp; //如果root为空结点，那么直接返回
			
        //分别求出左子树和右子树对应的dp数组
		auto dpl = dfs(root->left, k); 
        auto dpr = dfs(root->right, k);
		//当i=0时
        dp[0] = *max_element(dpl.begin(), dpl.end()) + *max_element(dpr.begin(), dpr.end());
		//当i >= 1时
        for (int i = 1; i <= k; ++i) {
            for (int j = 0; j < i; ++j) {
			   //更新dp[i]
                dp[i] = max(dp[i], root->val + dpl[j] + dpr[i - j - 1]);
            }
        }
        return dp;
    }
};

其实无论是树形dp还是线性dp，解决问题最重要的步骤就是求出状态转移方程。

Reference:

• 二叉树染色
• 树形DP