最近在研究三维物体非刚性配准的问题,这篇博客里讨论了一个比较传统的方法,然而现在机器学习才是大势所趋。我对机器学习实在是知之甚少,看paper看得我脑袋都大了……最近在读老师给我的论文,作者在文章中提到了他们在数年前在SIGGRAPH上发表的一种关于物体实时变形的论文:Bounded Biharmonic Weights for Real-Time Deformation,提出了一种通过用户交互来使物体变形的方法。本篇博客是关于这篇论文的笔记。
方法概述
这篇文章提出的bounded biharmonic weight(以下以BBW为简称)可以在约束条件下最小化拉普拉斯能量。关于拉普拉斯能量这个概念,文章中并没有详细说明,不过我觉得可以参考拉普拉斯矩阵的定义。拉普拉斯矩阵存储了三维物体中每个点与其邻域点之间的距离。当我们对物体进行变形的时候,需要保证变形之后的物体看上去比较顺眼(比如表面上不能坑坑洼洼)。由此可知,物体虽然整体上有明显的变形,但局部的变形不大,即每个点和其邻域之间的相对位置变动不能够太明显。因此,通过尽量减小这种点与点之间距离的变动(当然不能完全不变,只是要限制在一个范围内),能够保证物体光滑。
很多变形方法,比如之前博客里提到的老古董自由变形,需要在物体外部构建一个封闭的框架(cage),如果待变形物体的形状比较复杂的话,会给框架的构建带来麻烦。而BBW对物体框架的封闭性并没有要求,它的框架实际上是一堆simplice(这个我不知道怎么翻译,只能意会了)的集合。
该方法的大体思路比较明确。首先在物体上设置$m$个控制句柄(control handle,这个handle可以是一个区域,一个点,或者一根骨骼线),用户可以拖动这些句柄,也就是对每个句柄进行一个仿射变换$T_j$。然后通过以下公式获取物体中每个点变形后的坐标:
\[p' = \sum_{j=1}^{m}w_j(p)T_jp\]其中,$w_j$是$T_j$的BBW。
而$w_j$的值是通过最小化拉普拉斯能量来获得的。相对应的求解模型如下(排版有点丑凑合看了):
\[\mathop{\arg\min}_{w_j,j=1,...,m} \sum^{m}_{j=1} \frac{1}{2} \int_{\Omega} \Vert \Delta w_j \Vert ^2dV\] \[s.t. \\ w_j \vert H_k = \delta_{jk} \\ w_j \vert F \quad is \quad linear, \forall F \in F_C \\ \sum_{j=1}^{m}w_j = 1 \\ 0 \leq w_j(p) \leq 1\]其中$H_k$代表一个控制句柄,$\delta_{jk}$是克罗内克函数,当$i=j$时值为1,否则值为0,这样的话能够保证在控制句柄处的BBW值是最大的。$F_c$是框架面(cage faces)的集合。
此外,BBW的值不可以小于0,因为如果出现负值,物体就会朝着相反的方向变形,那就不符合常理了。
由此求得的图形能够保留许多特性。首先最小化拉普拉斯能量能够使变形后的物体是平滑的,其次,每个$w_j$在其对应的控制句柄处是最大的,并随着点到控制句柄的距离的增加而减小,就像下图姜饼小人的heat map所示。换言之,对某一处点的拖动只能影响他周围的局部形状。

实现
在实际实现的时候,作者采用了线性有限元(linear FEM)来将$w_j$的求解公式进行了离散化。部分的实验结果如下:
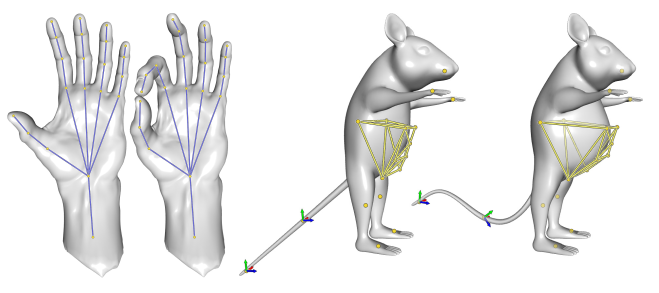
可以看出,物体框架可以是局部的或者非封闭性的,并且拖动某一个局部部分并不会影响到其他部分的形状。结果整体上也很自然。