最近在忙各种各样的事情,忙着改代码写论文还有准备找工作,连游戏都没空碰(啊,好想玩侠客风云传……),所以转眼间又大半个月没写博客了。
寻思着总得写点什么,想到我对图论相关的算法一直都不太熟(虽然研一的时候选过图论相关的选修,但是都是纸上谈兵),于是这篇博客的主题是图论中很常用的拓扑排序。内容包括拓扑排序的简要概括,以及一些相关的leetcode困难题的题解。
浅尝一下拓扑排序
简单地来说,拓扑排序就是对一个有向无环的图的顶点进行排序,它可以分为三步:1. 找到入度为0的点并输出,2. 删除这些点以及连着它们的边, 3. 重复1和2直到所有的点都被删除。
这可以用深度优先搜索(DFS)或广度优先搜索(BFS)来实现。
这两种方法首先都需要建图,首先获取从每个点出发的edge所指向的点,以及每个点的入度。
如果用DFS,那么用一个栈存储来点的排序。首先访问图中的任意一点,并依次访问它的邻接点,同时记录每个点的访问情况。如果一个点的所有的邻接点都被访问过了,那么该点被标记为已访问,并被压入栈中,这样一来,最后被压进栈里的就是入度为0的点,应该被排在最前面。
如果用BFS,那么首先建立一个队列,并将入度为0的点入队,然后:当队列非空时,将最前面的点出队,并将其邻居点的入度-1,如果邻居中有点的入度变为了0,那么将其入队。这个步骤会被不断地重复,直到队列为空(此时要么所有的点都排序完毕,要么图里有环,无法排序)
浅尝一下例题
例题1:外星文字典
以下是剑指offer上的一道困难题:外星文字典,因为题目有点长,我直接放上截图:

简单地来说,就是这门外星语言有一个独特的字典序,给出一些按照外星字典排序的单词,我们需要根据这些单词推测出其中的字母在外星字典里的前后顺序。
在单词中出现的字母可以被视为图中的一个结点,而有明显先后顺序的字母之间存在边,例如,由于”wrt”排在”wrf”之前,说明”t”应该在”f”前,那么图中就存在一条从”t”指向”f”的边。
解这道题的方法是:首先通过比较两两相邻的单词来获得字母之间的相对顺序,构造出一个有向图,然后再进行拓扑排序。
需要注意的是,题目中提到这个外星字母的排序可能会有问题(也就是有向图中存在环),因此我们在拓扑排序的过程中也要注意结果是否合理。
以下是用BFS实现拓扑排序的代码:
class Solution {
public:
unordered_map<char, vector<char>> edges; //记录边
unordered_map<char, int> indegrees; //入度
bool valid = true;
//构建图
void add_edge(string word1,string word2)
{
if(!valid)
return;
//遍历两个单词,找到第一个不同的字符
int n = word1.size();
int m = word2.size();
int idx = 0;
while(idx < n && idx < m)
{
//说明此时c2排在c1之后
if(word1[idx] != word2[idx])
{
char c1 = word1[idx];
char c2 = word2[idx];
edges[c1].push_back(c2);
indegrees[c2]++;
break;
}
idx++;
}
//排序有问题
if (n > m && idx == m) {
valid = false;
}
return;
}
string alienOrder(vector<string>& words) {
int length = words.size();
//初始化哈希表
for (auto word : words) {
int wordLength = word.size();
for (int j = 0; j < wordLength; j++) {
char c = word[j];
if (!edges.count(c)) {
edges[c] = vector<char>();
}
}
}
//构建图
for (int i = 1; i < length && valid; i++) {
add_edge(words[i - 1], words[i]);
}
if (!valid) {
return "";
}
queue<char> qu;
for (auto it : edges) {
//入度为0的字母(排序是靠前的)
if (!indegrees.count(it.first)) {
qu.emplace(it.first);
}
}
string order;
while (!qu.empty()) {
char u = qu.front();
qu.pop();
order.push_back(u);
//将与u相连的字母放入队列
for (char v : edges[u]) {
indegrees[v]--;
if (indegrees[v] == 0) {
qu.emplace(v);
}
}
}
return order.size() == edges.size() ? order : "";
}
};
例题2:矩阵中的最长递增路径
题目:
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
一个例子:
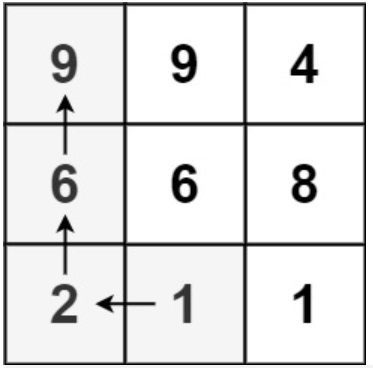
题解:
我们可以将这个矩阵化为一个有向图,如果矩阵中的一个元素比它的某个邻居要小,那么就构造一条由该点指向邻居的边。对于矩阵中每个元素,我们统计它的出度(即周围有几个点的值比它大)。
对于出度为0的点,它周围没有任何比它大的点,所以该点必定是某条递增路线的终点。我们可以采用BFS来解决这个问题。首先建立一个队列,将出度为0的点存入其中。当队列非空时,循环执行这样的操作:对于当前队列中的每个元素,依次取出队列最前端的点,搜索其四周是否存在值小于该点的邻居,如果存在,就将邻居点对应的出度值减一(周围有一个比它大的点被访问过了),如果邻居点的出度变为了0,就将其放入队列中。
每进行一次循环,代表递增序列的长度增加1,因此最长递增序列的长度等于循环的次数。
以下是用BFS解题的代码:
class Solution {
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
//dirs代表上下左右,由于连续打2个大括号jekyll会报错,所以略过了定义
//不知道有什么方法可以解决这个问题
int dirs[4][2];
int m = matrix.size();
int n = matrix[0].size();
//建立有向图
//统计出度,即四周比自身更大的邻居的数量
vector<vector<int>> outdegree(m,vector<int>(n,0));
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
for (int k = 0; k < 4; ++k) {
int newRow = i + dirs[k][0], newColumn = j + dirs[k][1];
if (newRow >= 0 && newRow < m && newColumn >= 0 &&
newColumn < n && matrix[newRow][newColumn] > matrix[i][j])
{
++outdegree[i][j];
}
}
}
}
queue<pair<int,int>> q;
//出度为0的点周围没有比它更大的点,所以其一定是某条路径的终点
//从出度为0的点开始搜索
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(outdegree[i][j]==0)
q.push({i,j});
}
}
int rtn = 0;
while(!q.empty())
{
int sz = q.size();
rtn++;
for(int i = 0; i < sz;i++)
{
auto pt = q.front();
q.pop();
for(int j = 0; j <4; j++)
{
int newx = pt.first+dirs[j][0];
int newy = pt.second + dirs[j][1];
if(newx >= 0 && newy >= 0 && newx < m && newy < n &&
matrix[newx][newy] < matrix[pt.first][pt.second])
{
outdegree[newx][newy]--;
if(outdegree[newx][newy] == 0)
q.push({newx,newy});
}
}
}
}
return rtn;
}
};
6.18日新增
在做图论专题的学习计划的时候碰到了一道新的题。
例题3: 找到最终的安全状态
有一个有 n 个节点的有向图,节点按 0 到 n - 1 编号。图由一个 索引从 0 开始 的 2D 整数数组 graph表示, graph[i]是与节点 i 相邻的节点的整数数组,这意味着从节点 i 到 graph[i]中的每个节点都有一条边。
如果一个节点没有连出的有向边,则它是 终端节点 。如果没有出边,则节点为终端节点。如果从该节点开始的所有可能路径都通向 终端节点 ,则该节点为 安全节点 。
返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按 升序 排列。
示例:
假设输入的是如下的一个图:
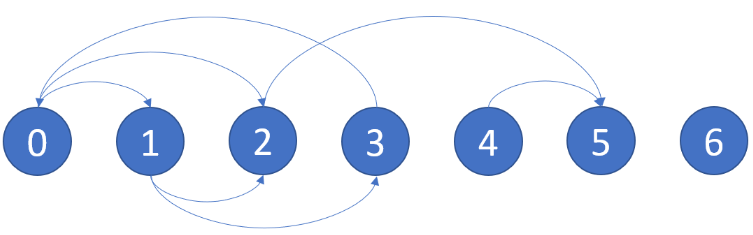
那么输出节点为[2,4,5,6]。
题解:
感觉题目描述挺绕的……其实可以把答案分为两部分:1. 出度为0的节点,2. 只与出度为0的节点相连的节点。将这两部分都求出来,排序后就得到了最终答案。
令初始的图为graph,我们首先把有向图里每条边的方向都翻转,得到新的图inverse_graph。这样的话,在graph中出度为0的点,到inverse_graph里就变成了入度为0的点。我们统计inverse_graph中每个节点的入度,用一个数组count来记录。
然后再采用拓扑排序,首先将inverse_graph中所有入度为0的点存入一个队列中,再在inverse_graph中依次删除这些节点。每删除一个节点,其相连的节点的入度值就要-1,如果由此产生了新的入度为0的点,就将其push到队列中,一直重复直到队列为空。在这个过程中所产生的的所有入度为0的节点就是符合条件的点。
代码如下:
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
//找到所有入度为0的点(反过来)
int n = graph.size();
vector<vector<int>> inverse_graph(n);
vector<int> count(n,0);
for(int i = 0; i < graph.size();i++)
{
for(int j: graph[i])
{
count[i]++; //计算入度
inverse_graph[j].push_back(i);
}
}
queue<int> q;
//找出入度为0的点
for(int i = 0;i < n;i++)
{
if(count[i] == 0)
{
q.push(i);
}
}
vector<int> rtn;
while(!q.empty())
{
int cur = q.front();
q.pop();
rtn.push_back(cur);
//与他相连的点入度-1
for(int i: inverse_graph[cur])
{
count[i]--;
if(count[i] == 0)
{
q.push(i);
}
}
}
sort(rtn.begin(),rtn.end());
return rtn;
}
};