之前一直在捣鼓一些有关点云非刚性配准的问题,现在转换了目标,开始研究网格模型的非刚性配准了。我主要是想要了解如何在保证网格表面平滑以及网格质量(比如说,不能有过于尖细的三角形)的情况下,来对source mesh朝着target mesh的形状进行变形。同时,我也想知道如何定义从source到target的所谓“距离”,也就是损失函数。我找来了一些论文,本篇博客是关于其中一篇发表在CVPR上的论文:3DN: 3D Deformation Network 的阅读笔记。
1. 方法
这篇文章提出的网络,简称为3DN,只改变顶点坐标,而不改变点之间的拓扑关系。输入有两部分,一个是source mesh,用$S=(V,E)$来表示,其中$V$是顶点集合,$E$是三角形的集合。另一个是source变形的参照对象$T$,即target,是一张二维的图像,或一个三维模型。我只想考虑target是三维模型的情况,此时$T$是一个三维点云,其点的数量为$N_T$。网络的输出是$S$中每个顶点的位移$O$。那么变形后的source mesh为$S=(V’,E)$,其中$V’ = V+O$。
3DN有一个source编码器和target编码器,用来学习source和target的全局特征,还有一个位移解码器,采用编码器的输出来求解形变。流程图如下:
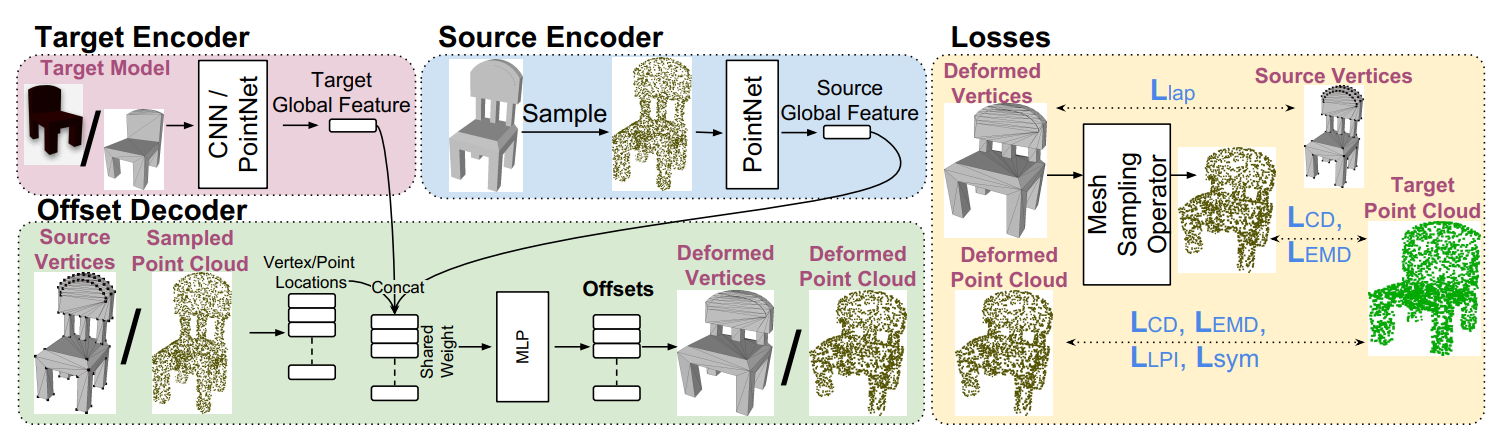
编码器
编码器的结构参考了PointNet, 其输入的数据是点云,所以对于source mesh,首先从表面均匀地采样一些点,再将这些点送入编码器中。编码器会输出一个全局特征向量(global feature vector)。source和target的特征向量被拼接在一起之后送入解码器。
解码器
解码器通过学习函数$F(\cdot)$来预测每个点的形变。输入一个三维坐标$v$,$F$能够预测出位移$o$,最终我们可以得到变形后的坐标$v’ = v+o$。解码器的设计同样参照了PointNet,不过与PointNet不同的是,解码器将顶点坐标与特征向量连接到了一起(PointNet里用的是单个点的特征)。
损失函数
我们需要一个损失函数来衡量$S’$和$T$之间的距离(这是我想要了解的重点)。作者提出了一个Differentiable Mesh Sampling Operator(DSMO),用来从网格的表面均匀采样点。
用质心坐标来表示从一个三角面片上采样的点$p = w_1v_1+w_2v_2+w_3v_3$,其中$w_1+w_2+w_3 = 1$,那么变形之后该点对应的偏移量也应该按照同样的权重来算,即$o_p = w_1o_{v_1}+ w_2o_{v_2}+ w_3o_{v_3}$。这样在反向传播的时候,顶点的梯度可以用$g_{o_{v_i}} = w_ig_{o_{v_p}}$来简单计算。
此外,作者采用了chamfer和earth-mover距离来衡量$S’$的采样点云$PC$和$T$的采样点云$PC_T$之间的误差。其中chamfer距离就是$PC$中每个点到$PC_T$的最近距离以及$PC_T$中每个点到$PC$的最近距离的平方之和。而earth-mover距离对我而言是个新的概念,它需要求得一个$PC \rightarrow PC_T$的点到点的映射,使每对点之间的距离之和最小,这个最小的距离即为earth-mover距离。这两种距离对于不同的点密度具有健壮性,分别用$L_{CD}$和$L_{EMD}$来表示。
除了以上这些内容之外,我们还需要一些其他的loss来保证$S’$的质量,因此作者还提出了以下的三个loss:
对称损失 Symmtry loss:
很多人造的物体是有对称性的,但是他的mesh拓扑不一定是对称的,所以在从source mesh上采样点云的同时,作者还对$S$的镜像模型进行了采样,获得镜像点云$M(PC)$,并借助它来计算对称损失:
\[L_{sym}(PC,PC_T) = L_{CD}(M(PC),PC_T)+ L_{EMD}(M(PC),PC_T)\]说白了就是对$M(PC)$和$PC_T$计算chamfer距离和earth-mover距离,以此来保证变形后模型的对称性。然而我对这个地方有点疑惑,这个loss似乎只能应用于严格对称的物体,并且对称轴是已知的才可以。此外,就算原模型$S$是对称的,但是$T$不一定对称,万一$T$就是一侧大另一侧小,那这个loss应该会阻止$S$往正确的方向变形吧?总觉得采用这个loss起作用的前提条件有些许苛刻。
拉普拉斯损失 Mesh Laplacian loss: 这个没啥好讲的,目的是为了保证$S’$表面平滑,其计算方法如下:
\[L_{lap} = \sum_{i} \|Lap(S)-Lap(S')\|_2\]其中$Lap()$是拉普拉斯算子。
局部置换不变损失 Local permutation invariant loss: 这个loss的目的是,让模型在变形过程中不会和自身相交。一些老旧的变形方法,比如自由变形(在之前的博客里探讨过),则无法保证这一特性。为了实现这一特性,对于一个点$p$以及距离它$\delta$的邻居点,需要保证二者的距离不受变形的影响:
\[L_{LPI} = -\min(F(V+\delta) - F(V),0)\]即二者形变程度相同,其中$\delta$是一个很小的三维offset。如果我们将变形前后的模型分成很多很小的部分,可以发现在这些小的局部范围内,点和点之间的相对距离的变动其实很小,因此这个loss也有助于保持表面的平滑性。这个概念在另一篇论文阅读笔记里也有提到过。
以上就是所有的loss的定义。对于$L_{CD}$和$L_{EMD}$,需要分别计算source是网格顶点和采样点云这两种情况下的结果。最后获得七个loss,每个都赋予权重,加起来就获得了最终的损失函数$L$。
2. 实验结果
实验的细节就懒得记笔记了。以下是3DN与其他的网络的实验结果对比。
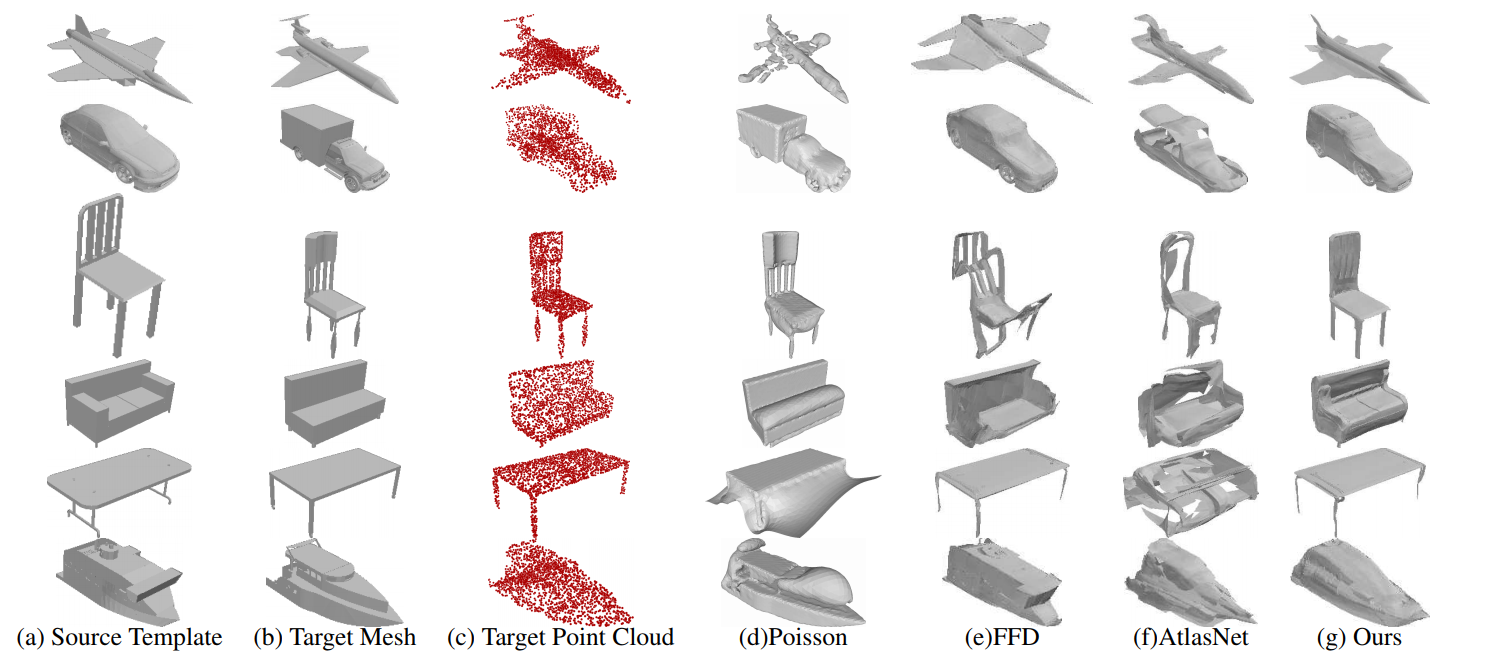
可以看出3DN的结果更加平滑,对称性更好。
3. 我的一些总结
这篇论文在神经网络结构上并没有花费太多笔墨,主要是借鉴了PointNet。作者对于loss的计算描述很详细,而这也是我最想要了解的部分,看完这篇论文收获还是挺多的。
有些其他论文会把三角面片的规则度(mesh regularity,我也不知道怎么表述,暂且就称之为规则度吧)也放入考虑范围内,比如就是让三角面片的三个角的大小差距不要太大,不要出现特别尖细的三角形等等,不过这篇论文似乎没有考虑到这一点。一个简单计算规则度的方法是,对于一个三角形的三条边,计算如下参数:
\[\gamma = \frac{4\sqrt 3 w}{l^2_1+l^2_2+l^2_3}\]其中$w$是三角形的面积。三角形越不规则,$\gamma$越小。当三角形为等边三角形时,$\gamma$达到最大值,为1。