居然有二十来天没有写博客了!
前一段时间一直在忙着写我的第二篇会议论文,终于在上周提交啦!今天正好是我到东京的第30天,我基本上已经适应在日本的生活了,只不过最近新冠疫情肆虐所以很少出门,大部分时间都在自己的小房间里待着。
在做本学期一门课遗留下来的作业的时候接触到了小波树这个结构,查了一下网上相关的资料并不是很多,不过还好有论文可以借鉴。
提到小波树,第一反应就是信号处理里的小波变换(wavelet transform)。小波变换递归地把信号分成高频和低频部分,而小波树的原理和它是类似的。小波树可以让我们在使用较少的空间的情况下,快速地对一系列数据进行排序以及查找。
小波树经常被用来压缩数据,一个简单的例子如下图所示:
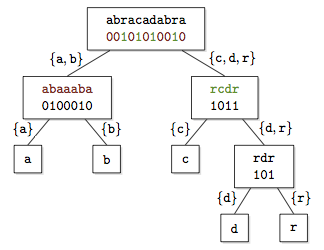
上图所示的小波树是一个平衡二叉树结构。我们用$S[1,n]$来表示图中的字符串,其中$n$表示$S$的长度,假设字符串中包含的字符种类为$\sigma$。图中的字符串序列由a,b,c,d,r这五个字母组成,因此$\sigma = 5$。
小波树的根节点存储了一串二进制数$B[1,n]$(bitmap),当字符串中的第$i$位小于字母表的前半段时,$B[i] = 0$,反之$B[i]=1$。然后我们根据这个方法,递归地对字符串进行分段,将对应值为0的子字符串分到左子树上,将对应值为1的子字符串分到右子树上,直到只剩下一种字母。
小波树的高度是$\lg \sigma$,其包含的非叶子节点数为$\sigma-1$,叶子节点数为$\sigma$。我们可以发现,小波树的每一层都存储了$n$个bit的数据。因此其存储的总数据量最多为$n\lg \sigma$。
我们可以从小波树来恢复整个$S$。在小波树中查询任意$S[i]$所需要的时间复杂度为$O(\lg\sigma)$。想要查询$S[i]$的值,我们首先获取小波树根节点处$B_{root}[i]$的值,若值为0,则查询它的左子树,若值为1,则查询它的右子树。以值为1为例,我们可以得知$B_{root}[i]$是$B_{root}$中从左到右数第$i_1$个1,那么下一步就从右子树存储的二进制串中查询$B_{right}[i_1]$的值,若值为0,则查询它的左子树,反之查询右子树。按照这样的方法依次递归到叶子节点即可获得$S[i]$对应的值。由于我们查询的节点个数即为小波树的高度,因此查询的时间复杂度为$O(\lg \sigma)$。
此外,如果我们从叶子节点向上查询,就可以得知每个字母在$S$中出现的位置以及次数。
小波树最常见的用途是压缩数据,这一部分大致已经在前面描述过了,但是还有很多细节我懒得写了(或许以后会加上来?我参考的这篇论文里解释得很详细)。在读论文的时候我发现小波树还可以用来表示一组点集,我对这个比较感兴趣。以下是关于小波树如何存储点集的说明。
假设我们在二维空间里有$n$个点,我们可以将这$n$个点映射到一个$n \times n$的离散网格上,其中任意2个点不在同一列或同一行上。我们用$(x_i,y_i)$来表示第$i$个点的坐标,点是按照$x$值从小到大的顺序来排列的。令字符串$S[1,…,n]=y_1,…,y_n$,并用小波树存储,按照前文所述的方法,我们可以通过访问$S[i]$来获取第$i$个点的坐标。此外,由于构建小波树的每一层都需要对数据进行二分,靠前的数据放入左子树,靠后的数据放入右子树,我们所得到的小波树的叶子节点从左到右看,是按照从小到大的顺序排列的。因此,如果我们从根节点向下查询,可以获取按照$x$值排列的第$i$个坐标,如果我们从叶子节点向上查询,那么可以获取按照$y$值排列的第$i$个坐标。
我们可以对小波树进行各种查询。以下是一个典型的例子:
查找在矩形范围的点
我们可以通过查询小波树来获取落在$[x_{\min},x_{\max}] \times [y_{\min},y_{\max}]$范围内的点的数量。首先我们从根节点处的bitmap找出区间$B_{root}[x_l,x_r]$,其中$x_l = x_{\min}$,$x_r=x_{\max}$。随后,我们将这个区间映射到左右两侧,即$x_l \leftarrow {\rm rank_{0/1}}(B_{root},x_l-1)+1$,$x_r \leftarrow {\rm rank_{0/1}}(B_{root},x_r)$,其中${\rm rank_a}(B,i)$求取的是值$a$在$B$的第1到i位里出现的次数。映射到左子树时,我们求取 ${\rm rank}_0$,映射到右子树时,我们求取的是${\rm rank}_1$。我们递归地对$x_l$和$x_r$进行上述的映射操作,可以获得很多小区间,直到满足以下三个条件中任意一个时停止递归:
-
$[x_l,x_r]$区间为空,代表落在查询范围内的点数为0。
-
$[x_l,x_r]$区间对应的点的$y$坐标与$[y_{\min},y_{\max}]$没有交集,同样表明落在查询范围内的点数为0。
-
$[x_l,x_r]$对应的$[y_l,y_r]$落在$[y_{\min},y_{\max}]$之内,此时这个子区间的点落在查找范围内,包含的点数为$(x_r-x_l+1)$。
递归查询的时间复杂度为$O(\lg n)$。对于范围内的每个点,我们可以继续向下查询来获取他们的具体坐标,每个点的查询时间为$O(\lg n)$。查找的过程大致如下图所示:
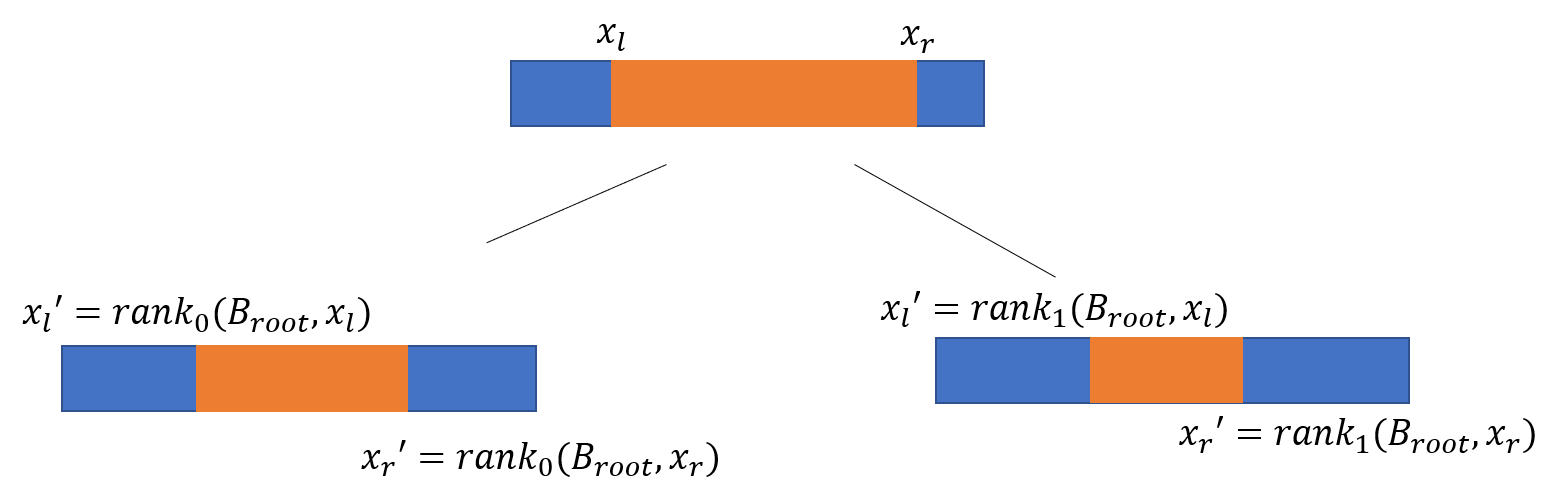
这类功能常常被用来解决计算几何的问题,也会被运用到GIS上。