这是秋招抱佛脚系列博客的第二篇，内容是关于基于物理的渲染（PBR）。PBR是一些在不同程度上都基于与现实世界的物理原理更相符的基本理论所构成的渲染技术的集合，在我之前的博客光线追踪里有所涉及，但是并不全面。

这篇博客的内容主要参考了LearnOpenGL网站上的教程。

PBR包括三个方面：基于物理的材质，基于物理的光照，基于物理适配的相机。可以通过以下三点来判断一个光照模型是否是基于物理的：

1. 基于微平面的表面模型。

2. 能量守恒。

3. 运用基于物理的BRDF。

1. 微平面模型

所有PBR模型都是基于微平面理论的，即当达到微观尺度时，任何平面都可以用一系列微小的镜面（即微平面）来描述。由此，平面越粗糙，其微平面的排列就越混乱，其入射光线的方向越发散，反射光线的分布范围也更加广泛。而平面越平滑，反射光线越统一。以下的图片可以解释这个情况：

我们可以假设一个粗糙度，并基于一个平面的粗糙度来计算出中间向量与微平面平均取向方向一致的概率。其计算方法如下：

其中$l$是光线向量，$v$是视线向量。微平面的取向方向与中间向量的方向越一致（即粗糙度越小），反射越强烈、锐利。

2. 能量守恒 反射率方程

根据能量守恒，出射光的能量不能超过入射光的能量，因此越是粗糙的平面，其镜面反射的光越黯淡。当入射光进入表面的时候，有一部分被折射（对应漫反射），另一部分被反射（对应镜面反射），折射光与物体内部的粒子发生碰撞之后，有一部分会再次离开表面，形成漫反射，如下图所示：

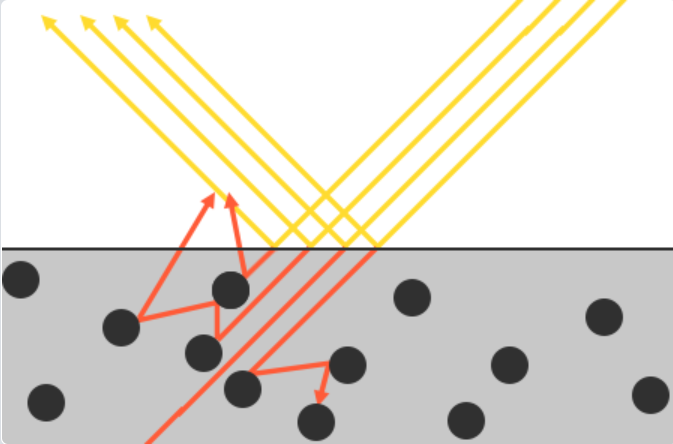
金属材料对光的反应和非金属（or介电质）材料是不一样的，金属材料的折射光会全部被物体表面吸收，不会产生漫反射。因此，金属和非金属材料在渲染管线中被分开处理。

PBR的实现是基于反射率方程的：

在看这个公式之前，先了解一些关于辐射度量学的知识。

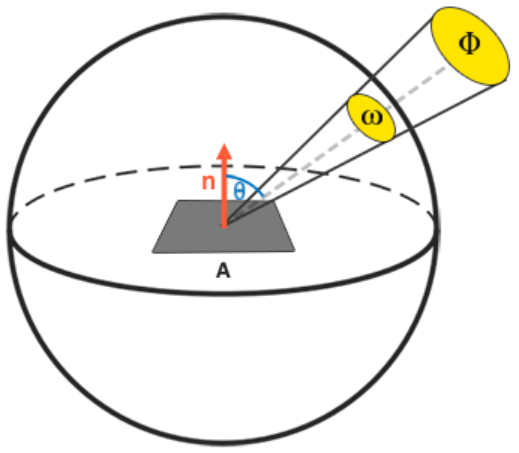
辐射通量$\Phi$：表示单位时间内穿过一个截面的光能，单位为瓦特。

立体角$\omega$：投射到单位球体上的截面的大小或体积。可以看做是一个带体积的方向。

关于这二者的解释如下图，其中$\theta$是光线方向向量和平面法线的夹角。

!<div align=center> </div>

辐射强度$I$：单位立体角上的辐射通量， $I=\frac{d\Phi}{d\omega}$。

辐照度$E$：单位面积上的辐射通量。

辐射率$L$：单位立体角、单位投影面积上的辐射通量。我们可以由以下公式计算辐射率：

当入射光完全垂直于平面时，其强度最高。如果把$A$和$\omega$看作无穷小，此时$A$可以看做一个点，$w$可以看做是一个方向向量。那么就可以根据以上公式计算出单束光线在单个点上的辐射率。实际中，我们关心的是所有投射到点p上的光线的总和，即辐照度。

此时对于$\theta$的计算：$\cos\theta = n\cdot w$

了解了以上信息之后，再回看反射率方程：

其中$p$为一个点，$\omega_o$指的是观察方向，$\omega_i$指的是光线的入社方向，$\Omega$的范围是一个半球。因此$L_o(p,\omega_o)$是在$\omega_o$方向被反射出来的辐射率的总和，也就是从$\omega_o$方向观察$p$点时，光线射到$p$被反射出的辐照度，通过按照一定的步长，对$\omega_i$积分来实现。以下是一段实现的代码：

int steps = 100;
float sum = 0.0f;
vec3 P    = ...;
vec3 Wo   = ...;
vec3 N    = ...;
float dW  = 1.0f / steps;
for(int i = 0; i < steps; ++i) 
{
    vec3 Wi = getNextIncomingLightDir(i);
    sum += Fr(p, Wi, Wo) * L(p, Wi) * dot(N, Wi) * dW;
}

式子中的$f_r$为双向反射分布函数(Bidirectional Reflective Distribution Function, BRDF)，它的作用是基于表面的材质属性来对入射辐射率进行缩放和加权。

3. BRDF

BRDF是基于1中所提到的微平面理论来近似得到材质的反射和折射属性的，同时也应该遵循能量守恒定律。它接收入射方向$\omega_i$，出射方向（or观察方向）$\omega_o$，平面法线$n$以及一个用于表示微平面粗糙度的参数$\alpha$作为输入，并输出每一束光线对给定材质平面的反射光的贡献程度。例如，对于镜面反射，只有出射光与$\omega_o$重合的时候BRDF函数会返回1，对于其他方向的入射光，BRDF的返回值为0。

Blinn-Phong模型也采用了$\omega_o$和$\omega_i$作为输入，但是它不是能量守恒的，因此并不是PBR。PBR中常用的光照模型是Cook-Torrance BRDF模型:

其中第一个部分为漫反射部分，$k_d$为漫反射比率，$f_{lambert}$被称为Lambertian漫反射。第二部分为镜面反射部分,$k_s$为镜面反射比率。$f_{lambert}$用下列式子表示：

其中$c$为表面颜色，$\pi$用于对漫反射光标准化。

镜面反射部分的公式如下：

其中分母是标准化因子，分子是三个函数的乘积，这三个函数分别为：法线分布函数(normal-distribution function)，菲涅尔方程(Fresnel equation)以及几何函数(geometry function)。

法线分布函数：从统计学上近似的表示了与某些（中间）向量$h$取向一致的微平面的比率。举例来说，假设给定向量$h$，如果我们的微平面中有35%与向量h取向一致，则法线分布函数或者说NDF将会返回0.35。以下是Trowbridge-Reitz GGX法线分布函数：

其中$h$为用于比较的中间向量，$\alpha$表示表面粗糙度。粗糙度越小，与中间向量取向一致的微平面会更加集中，从而形成一个很亮的小斑点，而粗糙度越大，微平面的取向变得更加随机，与中间向量趋向一致的微平面的范围会扩大，从而让结果发散的同时，变得更加的黯淡。

几何函数：从统计学上近似求得微平面之间相互遮蔽的比率。如下图所示：

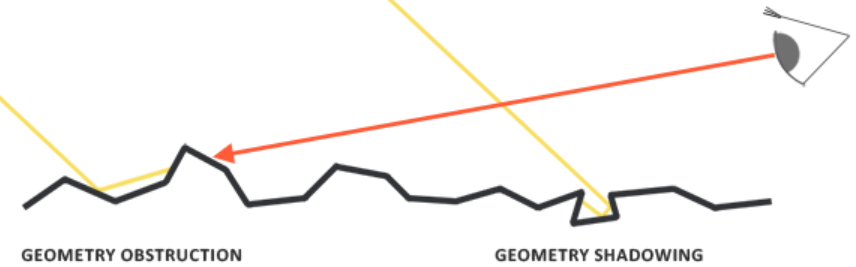
表面越粗糙，相互遮蔽率越大，以下是用于估算的Schlick-GGX函数：

$k$是$\alpha$基于几何函数针对直接光照或IBL光照的重映射：

此外，我们需要将观察方向$v$（几何遮蔽）和光线方向向量$l$（几何阴影）全都考虑进去，可以通过史密斯法来将两者结合：

菲涅尔方程：表示不同的入射角，反射率不同，返回一个反射光线所占的比例（反射率）。菲涅尔方程可以通过Fresnel-Schlick近似法来近似求解：

$F_0$表示基础反射率，从不同的方向观察平面，反光的明显程度会不一样。视线和表面发现的夹角越接近90度，菲涅尔现象越明显，反光越强。

对于金属材料，其基础反射率一般介于0.5和1之间，而且是带有色彩的，因此要用一个三维向量来表示。

基于以上三种方程，我们最终得到的cook-torrance BRDF方程如下：

第一个括号里的两部分分别是漫反射部分和镜面反射部分。

BRDF的计算：

我们可以将BRDF方程划分成两个卷积：

以下是我从网友的博客里copy来的内容，我觉得他总结得很好。

其中第一部分为预滤波环境贴图，将不同粗糙度的卷积结果存在不同的Mipmap中（不同的粗糙度对应着不同的mipmap级别，处于中间程度的粗糙度可以插值)，渲染时可以通过mipmap级数直接去采样对应的贴图得到积分结果。

第二部分称为BRDF部分，它可以进一步拆分为菲涅尔项有关的两部分，分别代表菲涅尔响应的比例和偏差，然后对这两项做卷积预计算，并存到一张查找贴图中(look-up texture，LUT)。渲染时可以将n·wi作为横坐标，以粗糙度roughness作为纵坐标，去LUT中采样获得该条件下的BRDF响应结果，以加快计算速度。

总结： PBR计算结果的漫反射部分，通过卷积存到一张辐照度图当中，该辐照度图是一个立方体贴图，表示了每一个出射光线采样得到的漫反射积分计算结果；镜面反射部分通过分割近似求和法，划分为两个卷积式子，第一部分计算结果存到一张预滤波环境贴图中，将不同粗糙度的卷积结果存在一张Mipmap贴图中；第二部分称为BRDF部分：以n·wi作为横坐标，以粗糙度roughness作为纵坐标，就可以从查找贴图中采样获得该条件下的BRDF响应结果。

Reference

• 【游戏开发面经汇总】- 图形学基础篇

• 理论